Оглавление:
Предел и непрерывность фнп
Рассмотрим функцию двух переменных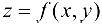 
.
Определение 11.1. Окрестностью радиуса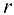 
точки 
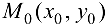называется совокупность всех точек 
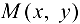удовлетворяющих неравенству
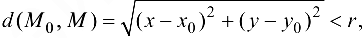
т. е. совокупность всех точек, лежащих внутри круга радиуса 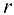с центром в точке .
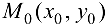В дальнейшем, говоря, что функция 
обладает каким-либо свойством «вблизи точки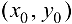 
» или «в окрестности точки», под этим будем подразумевать, что найдется такой круг с центром 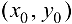, во всех точках которого данная функция обладает указанным свойством.
Пусть функция определена в некоторой области D плоскости 
. Рассмотрим некоторую определенную точку 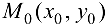, лежащую в области D или на ее границе.
Определение 11.2. Число А называется пределом функции 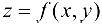при стремлении точки 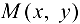к точке 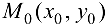(или при 
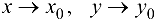, если для 
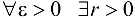, такое, что для всех точек 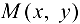, удовлетворяющих условию 
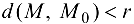, будет выполнено: 
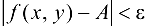. Обозначение:
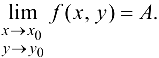
Пример 11.1.
Найти предел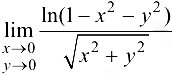 
Решение:
Обозначим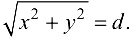 
Условие 
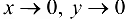равносильно тому, что 
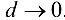. Получим
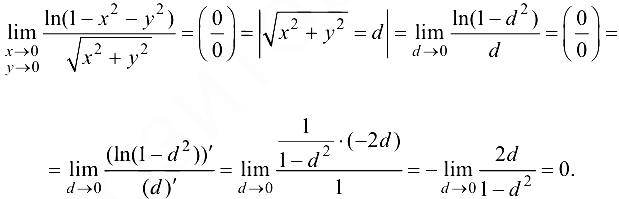
Ответ: 0.
Вычисление пределов функций двух переменных, как правило, оказывается более трудной задачей по сравнению со случаем функций одной переменной. Причина состоит в том, что па прямой существуют всего два направления, по которым аргумент может стремиться к предельной точке — а именно, справа и слева. На плоскости же таких направлений бесконечное множество и пределы функций по разным направлениям могут не совпадать.
Пример 11.2.
Доказать, что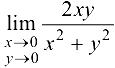 
не существует.
Решение:
Будем приближаться к точке (0;0) по прямым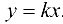 
.
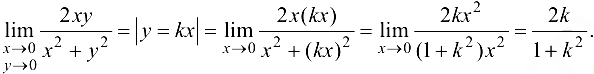
Таким образом, значение предела зависит от углового коэффициента прямой. Но, так как предел функции не должен зависеть от способа приближения точки 
к точке (0;0), то рассматриваемый предел не существует.
Ответ: предел не существует.
Замечание 11.1. Для функции 
переменных 
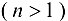можно рассматривать 
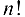, так называемых повторных пределов. В частности, в случае функции двух переменных 
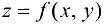можно рассматривать два повторных предела в точке 
:
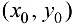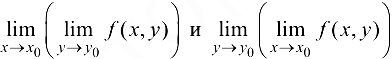
Пример 11.3.
Вычислить повторные пределы функции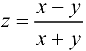 
в точке (0;0).
Решение:
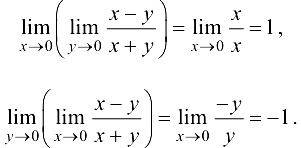
Вывод. Так как повторные пределы конечны, по имеют различные значения, то при вычислении повторных пределов порядок следования предельных переходов по разным значениям влияет на результат.
Определение 11.3. Функция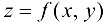 
называется непрерывной в точке 
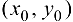, если она:
1) определена в точке ;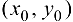
2) имеет конечный предел при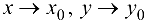 
;
3) предел равен значению функции в точке, т. е.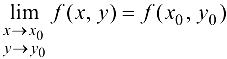 
.
Нарушение любого или нескольких из условий определения дает точку разрыва функции.
Геометрический смысл непрерывности состоит в том, что график функции в точке 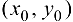представляет собой сплошную не расслаивающуюся поверхность.
Пусть переменной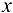 
дано приращение 
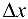, а переменная 
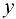оставлена неизменной. Тогда разность
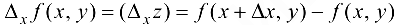
называется частным приращением функции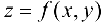 
по переменной .
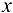Если неизменной остается переменная 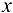, то разность
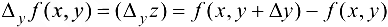
называется частным приращением функции 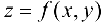по переменной .
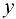В случае, когда обе переменные 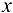и 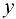получают соответствующие приращения 
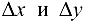, приращение функции
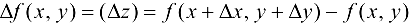
называется полным приращением функции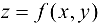 
.
Естественно, при определении данных понятий рассматриваются лишь такие точки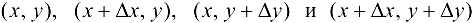 
, для которых функция 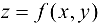определена.
Из формул (11.1), (11.2) и (11.3) следует, что
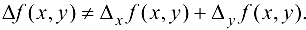
Пример 11.4.
Найти полное и частные приращения функции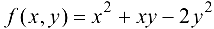 
, если х изменяется от 2 до 2,2, у изменяется от 1 до 0,9.
Решение:
Вычислим значения функции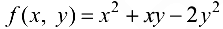 
в точках (2; 1), (2,2; 1), (2; 0,9) и (2,2; 0,9). Получим
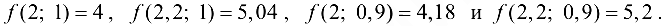
Тогда
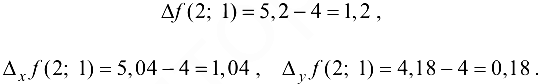
Так как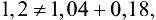 
, то имеем случай
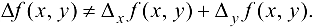
Ответ: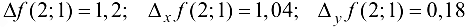 
.
Определение 11.4. Функция 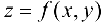называется непрерывной в предельной точке 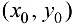из области определения функции, если
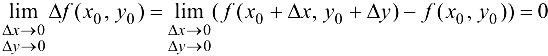
Заметим, что предельной точкой области определения называется точка, для которой функция определена как и в ней самой, так и в некоторой ее окрестности.
Определение 11.5. Функция 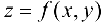называется непрерывной в области D, если функция непрерывна в каждой точке рассматриваемой области, т. е. если для каждой точки 
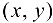области выполнено:
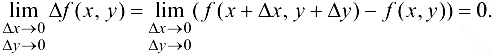
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
