Определение 6.1. Функция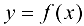 
называется дифференцируемой в точке 
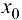, если ее приращение в этой точке 
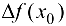может быть представлено в виде
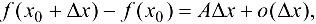
где А — некоторое действительное число, а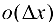 
— бесконечно малая функция более высокого порядка малости, чем 
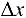при 
.
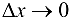
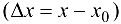Теорема 6.1. Для того чтобы функция 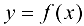была дифференцируемой в точке 
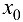, необходимо и достаточно, чтобы в точке 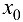существовала конечная производная 
.
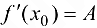Доказательство.
Необходимость. Если функция 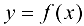дифференцируема в точке х0, то из определений 6.1 и 5.1
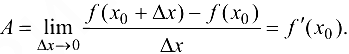
Достаточность. Если 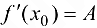, то по теореме 5.1 в окрестности точки 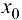справедливо равенство
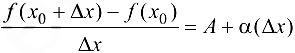, где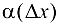 
— БМФ при 
.
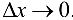Умножив обе части равенства на 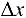получим (6.1). ■
С учетом теоремы 6.1 и равенства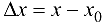 
, формулу (6.1) можно переписать в виде
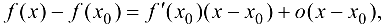
откуда при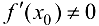 
получим
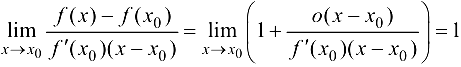
Следовательно, при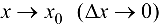 
будем иметь
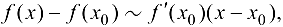
где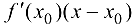 
называется главной линейной относительно приращения переменной 
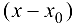частью приращения функции 
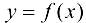при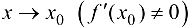 
.
Определение 6.2. Главная линейная часть приращения функции 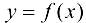в точке 
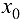называется дифференциалом 
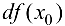функции в этой точке, т. е. 
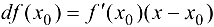или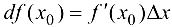 
. Если 
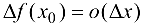, т. е.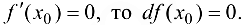 
Заметим, что если рассмотреть функцию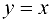 
, то в этом случае 
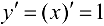и, следовательно, 
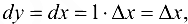т. е. дифференциал и приращение независимой переменной равны между собой: 
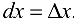. Поэтому дифференциал функции 
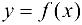в точке 
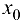можно представить в виде
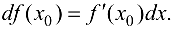
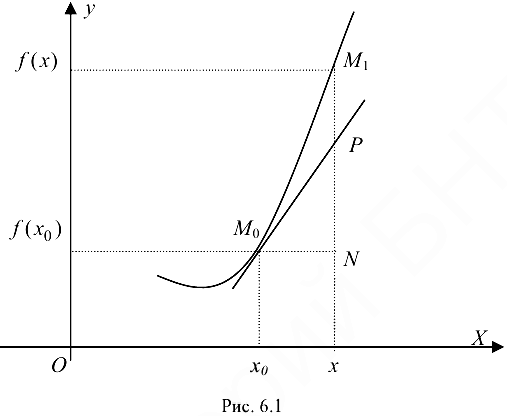
Геометрический смысл дифференциала следует из формулы (6.2), рис. 6.1. Согласно принятым обозначениям:
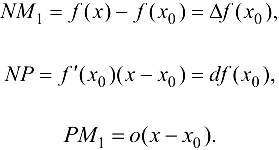
Дифференциал функции равен приращению NP ординаты касательной, проведенной к графику функции в точке с абсциссой 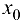при приращении аргумента 
.
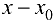Правила вычисления дифференциала аналогичны соответствующим правилам нахождения производной:
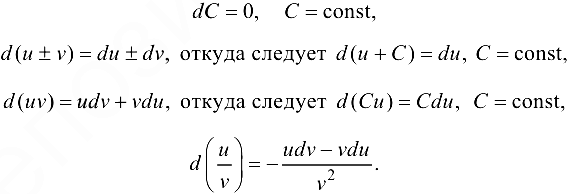
Пусть для функции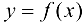 
переменная 
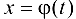. Если рассматривать 
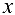как независимую переменную, то 
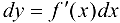, где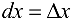 
. Если рассматривать как независимую переменную 
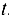, то
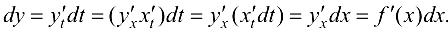
Таким образом, форма записи дифференциала сохраняется, если независимую переменную заменить некоторой функцией. Это свойство называется инвариантностью (неизменностью) формы записи дифференциала.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
