Геометрический смысл производной функции в точке
Пусть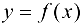 
— непрерывная функция, определенная в некоторой окрестности точки 
.
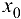Рассмотрим две точки графика этой функци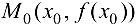и: 
и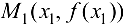 
. Прямая 
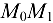— секущая 
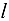(рис. 5.1). Обозначим:
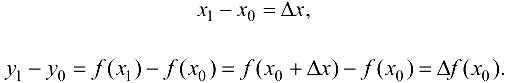
Найдем угловой коэффициент этой прямой. Из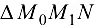 
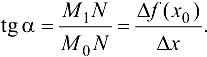
Из (5.1) следует, что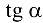 
зависит только от 
.
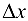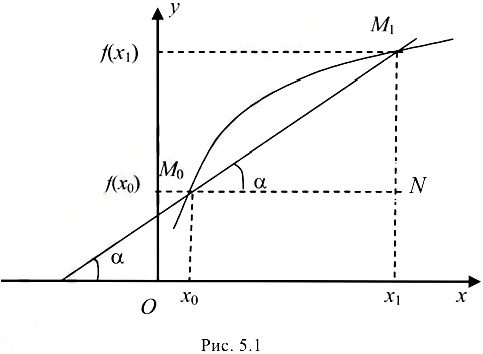
При перемещении точки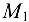 
к точке 
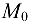по графику непрерывной функции 
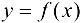, секущая 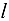будет стремиться к некоторому предельному положению: касательной к графику функции 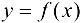в точке .
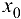Так как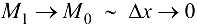 
, то угловой коэффициент касательной, проведенной к графику функции 
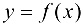в точке 
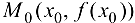, можно получить предельным переходом из (5.1):
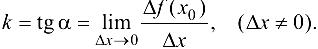
Уравнение касательной, как известно, определяется формулой
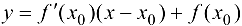
Вывод. Производная функции 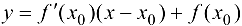в точке 
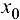равна угловому коэффициенту касательной, проведенной к графику функции в точке 
—
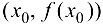Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
