Оглавление:
Пусть функция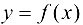 
определена на некотором множестве X. В качестве множества X можно рассматривать: 
, 
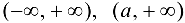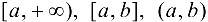и др.
Определение 3.1. Число А называется пределом функции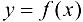 
в точке 
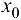, если функция определена в некоторой проколотой окрестности точки 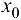, и если для 
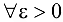найдется 
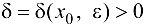, такое, что для любых х удовлетворяющих условиям 
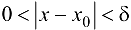, будет выполнено 
.
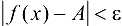Таким образом,
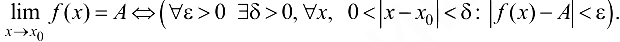
Данное определение предела функции в точке называется определением предела по Коши.
Пример 3.1.
Для функции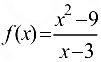 
найти предел в точке 
.
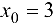Решение:
Так как при вычислении предела в точке 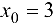сама точка в расчет не принимается 
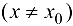, то
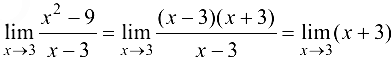
Докажем, что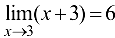 
. Для этого зададим 
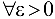и в соответствии с формулой (3.1) рассмотрим разность 
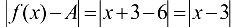. Полагая 
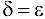, получаем, что как только 
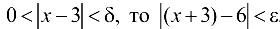. Таким образом, 
.
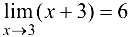Ответ: 6.
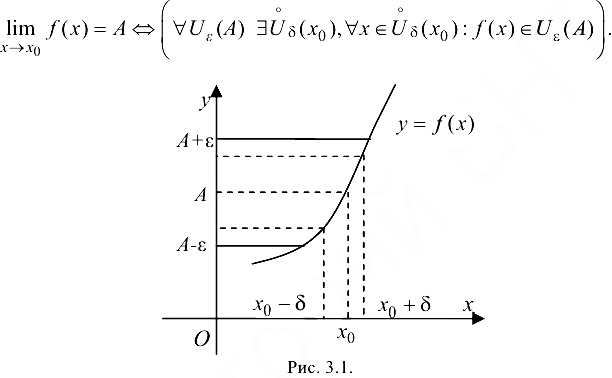
Геометрический смысл определения предела функции в точке: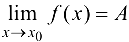 
, если для любой с-окрестности точки А найдется про-колотая 
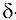-окрестность точки 
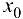, такая, что для всех 
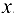из этой окрестности значения 
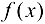будут принадлежать 
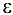-окрестности точки А (рис. 3.1), т. е.
Определение 3.2. Число А называется пределом функции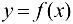 
в точке 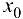, если функция определена в некоторой проколотой окрестности точки 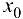и если для любой последовательности 
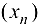, сходящейся к 
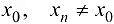, соответствующая последовательность значений функции 
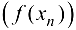сходится к А при 
.
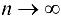Таким образом,
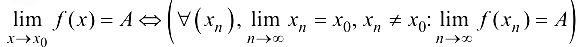
Данное определение предела функции в точке называется определением предела по Гейне.
Пример 3.2.
Используя определение предела функции по Гейне, доказать, что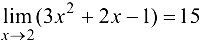 
.
Решение:
Рассмотрим функцию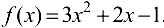 
. Возьмем произвольную числовую последовательность 
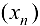, сходящуюся к 2, с членами, принадлежащими 
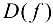и отличными от 2: 
.
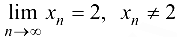Рассмотрим соответствующую последовательность значений данной функции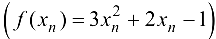 
. Докажем, что эта последовательность сходится к 15:
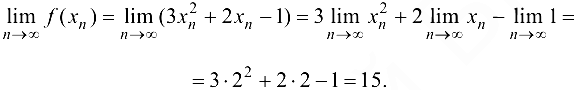
Таким образом, по определению предела функции по Гейне, имеем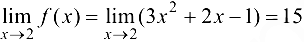 
. ■
Теорема 3.1*. Определения предела функции в точке по Коши и по Гейне эквивалентны.
Из определения предела функции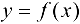 
в точке 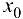следует, что сама точка 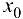исключается из рассмотрения, а функция считается определенной в некоторой достаточно малой окрестности точки 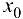. Существование предела функции в точке является локальным свойством функции.
Пусть аргумент функции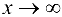 
, т. е. возрастает по модулю.
Определение 3.3. Число А называется пределом функци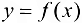и 
при 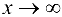, если 
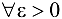найдется 
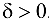, такое, что для любых 
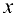, удовлетворяющих условию 
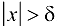, будет выполнено 
.
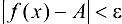Таким образом,
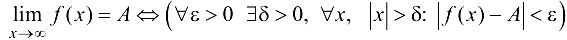
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Сходящиеся последовательности с примером решения |
| Свойства сходящихся последовательностей с примерами решения |
| Односторонние пределы с примером решения |
| Свойства функций, имеющих предел |
