Грани числовых множеств
Говорят, что множество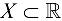 
ограничено сверху (снизу), если существует такое число 
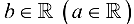, что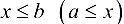 
для любого 
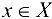. Число 
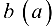в этом случае называется верхней (нижней) гранью множества X.
Множество, ограниченное и сверху, и снизу, называется ограниченным, т. е. существуют два числа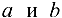 
, такие, что 
, 
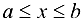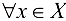. Эти неравенства показывают, что множество X ограничено в том и только в том случае, если оно расположено на некотором конечном отрезке числовой прямой. Очевидно, что множество X ограничено тогда и только тогда, когда существует положительное число С, такое, что
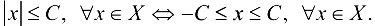
Множество, не ограниченное сверху или снизу, называется неограниченным.
Если число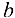 
является верхней гранью множества X, то и любое число больше 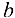тоже является верхней гранью, и, если число 
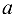-нижняя грань множества X, то всякое число, меньше 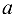будет нижней гранью X.
Наименьшая (наибольшая) из всех верхних (нижних) граней называется точной верхней (нижней) гранью множества и обозначается символом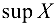 
(«супремум X») (
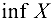, «инфимум X»).
Точные верхняя и нижняя грани множества могут принадлежать или не принадлежать этому множеству. Если множество X не ограничено сверху (снизу), то иногда используют обозначение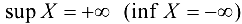 
.
Теорема 1*. Всякое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Элементы теории множеств: основные понятия |
| Логические символы в теории множеств |
| Предельные точки числового множества |
| Функция |
