Механическая система (рис. Д5) приводится в движение постоянной силой

Курсовая работа Д5

Дано:

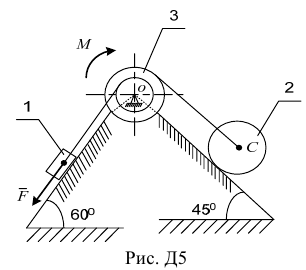
Механическая система (рис. Д5) приводится в движение постоянной силой

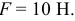
Масса тел соответственно:

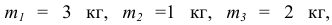
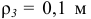
(радиус инерции третьего тела);

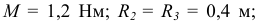
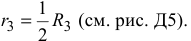
Каток 2 — сплошной однородный цилиндр. Определить ускорение первого тела .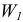

Решение

Решение задачи с помощью общего уравнения динамики Построим расчетную схему (рис. Д5а), где покажем задаваемые силы: 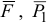— сила тяжести первого груза, 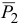— сила тяжести второго груза, 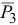— сила тяжести третьего груза; реакции внешних связей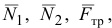 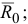; приложим приведенные силы инерции:

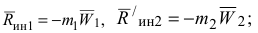
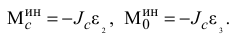
Приведенные силы инерции тел зависят от вида их движения тела (см. принцип Даламбера).

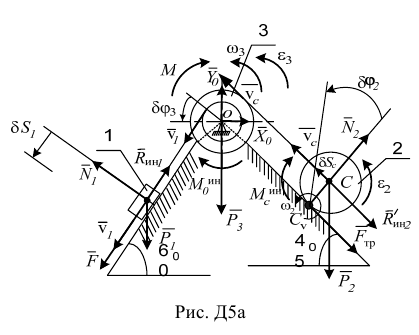
Выразим скорости, ускорения, перемещения всех тел через скорость, ускорение и перемещение тела 1.

Угловая скорость третьего тела равна 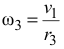(нить нерастяжима, все точки нити имеют одинаковые скорости).

Угловое ускорение третьего тела найдем следующим образом:

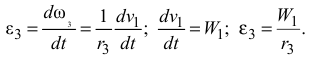
Возможное перемещение 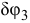блока 3 выразим через возможное перемещение 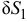первого тела по формуле

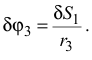
Перейдём ко второму телу

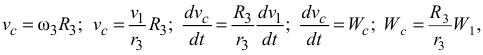
где 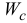— ускорение центра масс второго тела.

Угловая скорость второго тела

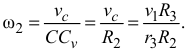
Продифференцировав по времени

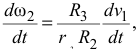
получим

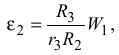
где 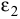— угловое ускорение второго тела.

Определим возможное перемещение 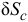центра масс и возможное перемещение 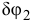катка 2 через возможное перемещение 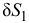первого тела

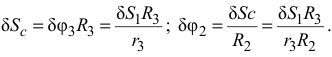
Определим приведенные силы инерции

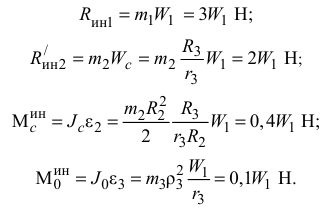
Сообщим системе возможное перемещение 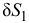и составим общее уравнение динамики:

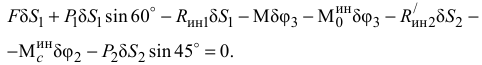
Подставив числовые значения заданных сил и сил инерции, а также значения перемещений, выраженных через 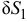, получим,

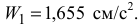
Ответ: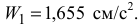

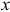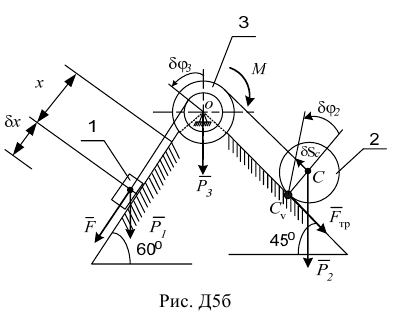
Решение задачи с помощью уравнения Лагранжа Данная система имеет одну степень свободы. Поэтому выберем одну обобщенную координату. Так как по условию требуется определить ускорение первого тела, которое совершает поступательное прямолинейное движение, выберем линейную обобщенную координату следящую за перемещением центра масс этого тела (рис. Д5б).

Запишем уравнение Лагранжа для данной системы

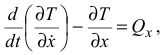
где 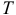— кинетическая энергия системы; 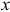— обобщённая координата; 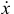— обобщённая скорость ;

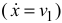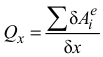— обобщённая сила;

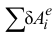— сумма элементарных работ внешних сил на приращении 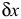заданной обобщённой координаты.

Определяем кинетическую энергию системы, выразив её через обобщенную скорость :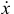

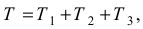
где 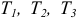— соответственно кинетические энергии первого, второго и третьего тел.

Первое тело совершает поступательное движение, его кинетическая энергия определяется по формуле

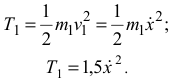
Второе тело совершает плоскопараллельное движение

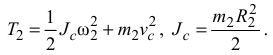
Зависимости скоростей точек системы мы рассматривали выше, когда выполняли это задание с помощью общего уравнения динамики

Подставив численные значения известных величин, получим:

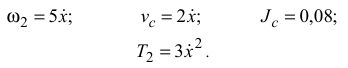
Третье тело совершает вращательное движение

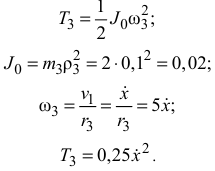
Таким образом, кинематическая энергия системы равна

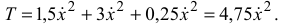
Дифференцируем полученные выражения согласно уравнению Лaгранжа

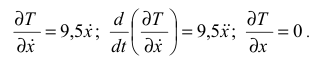
Определим обобщённую силу, для этого покажем на рис. Д5б внешние силы:

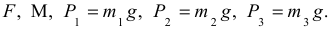
Сообщим приращение 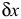выбранной обобщённой координате 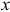и определим элементарную работу действующих сил

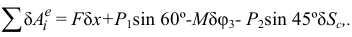
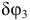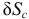Выразим и через 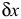(см. общее уравнение динамики).

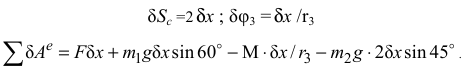
Подставив численные величины, получим:

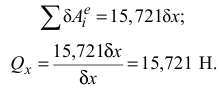
Найденные значения подставим в уравнение Лагранжа

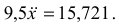
Следовательно,

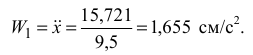
Сравнив результаты определения ускорения первого тела различными способами, делаем вывод: расчёт проведен верно.