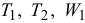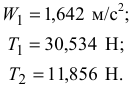Курсовая работа Д4
Дано:
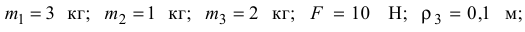
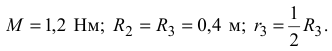
Определить: 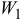 — ускорение первого тела, а также натяжение нитей на всех участках.
— ускорение первого тела, а также натяжение нитей на всех участках.
Решение
Для определения реакций связей воспользуемся принципом Даламбера.
Построим расчетную схему (рис. Д4), на которой покажем активные силы, реакции связей и приведенные силы инерции. На груз 1 действуют сила 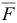 , сила тяжести
, сила тяжести 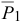 , реакция поверхности
, реакция поверхности 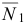 и равнодействующая сил инерции
и равнодействующая сил инерции 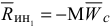 . Вектор
. Вектор 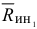 направлен в противоположную сторону вектора
направлен в противоположную сторону вектора 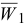 .
.
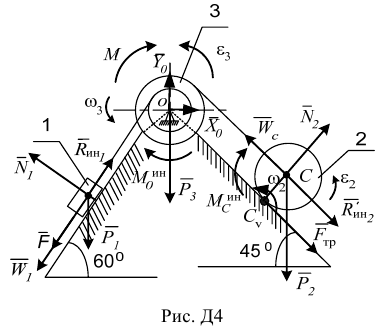
На ступенчатый блок 3 действуют сила тяжести 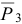 , реакции
, реакции 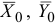 в шарнире
в шарнире 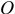 , пара сил
, пара сил 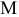 и главный момент сил инерции
и главный момент сил инерции 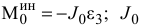 — момент инерции ступенчатого блока относительно оси вращения, проходящей через точку
— момент инерции ступенчатого блока относительно оси вращения, проходящей через точку 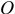 перпендикулярно плоскости рисунка
перпендикулярно плоскости рисунка
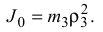
Выразим угловое ускорение ступенчатого блока 3 через ускорение первого груза. Зависимость скоростей
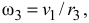
продифференцируем эту формулу по времени
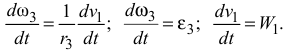
Получим
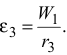
Подставив значение 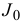 и
и 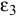 в уравнение главного момента сил инерции, получим:
в уравнение главного момента сил инерции, получим:
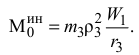
Главный момент сил инерции направлен в сторону, противоположную угловому ускорению ступенчатого блока.
На каток 2 действует сила тяжести 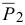 , реакция связи
, реакция связи 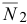 , сила трения
, сила трения 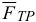 , главный вектор сил инерции
, главный вектор сил инерции 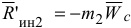 и главный момент сил инерции
и главный момент сил инерции 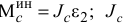 — момент инерции относительно оси, проходящей через центр масс перпендикулярно к плоскости движения.
— момент инерции относительно оси, проходящей через центр масс перпендикулярно к плоскости движения.
Выразим 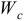 и
и 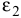 через
через 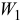 . Запишем формулы зависимости скоростей тел 1 и 2 (см. задачу Д2).
. Запишем формулы зависимости скоростей тел 1 и 2 (см. задачу Д2).
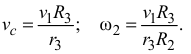
Дифференцируя эти зависимости по времени, получим:
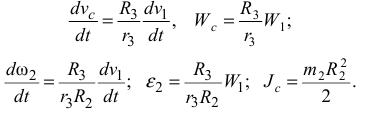
Тогда имеем
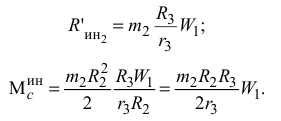
Для определения реакций нитей рассмотрим динамическое равновесие отдельных тел, входящих в систему.
Для каждого тела составим расчетные схемы (рис. Д4 а, б, в).
Задача сводится к определению реакций нити 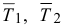 и ускорения первого тела
и ускорения первого тела 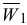 . Для трех неизвестных величин надо составить три уравнения равновесия.
. Для трех неизвестных величин надо составить три уравнения равновесия.
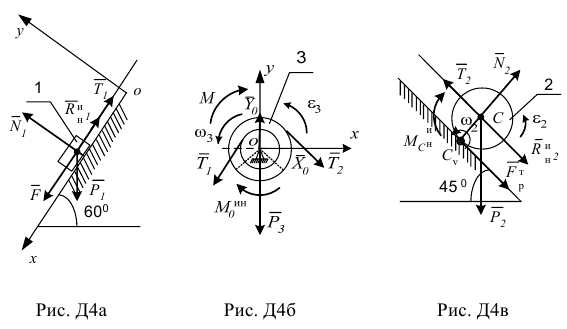
Для тела 1 (рис. Д4 а) составим уравнение 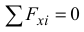
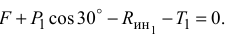
Для тела 3 (рис. Д4 б) составим уравнение 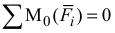
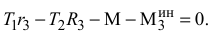
Для тела 2 (рис. Д4 в) составим уравнение 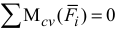
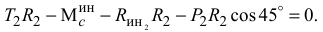
Подставив в уравнения (1), (2) и (3) значения приведенных сил инерции, получим:
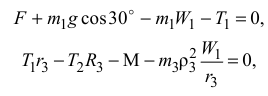
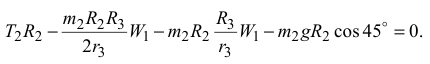
Подставив в уравнения (4) все численные значения, получим систему уравнений:
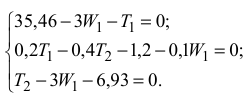
Решая эту систему уравнений, определим