Удар по вращающемуся телу
При исследовании удара по вращающемуся телу, кроме теоремы об изменении количества движения, приходится использовать и теорему об изменении момента количества движения (XIX, §3). Относительно оси вращения (19.19) её запишем так:
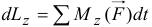
и после интегрирование за время удара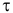 
получим
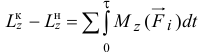
или
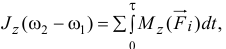
где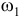 
и 
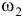— угловые скорости тела в начале и в конце удара; 
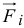— ударные силы.
Правую часть надо немного преобразовать. Найдем сначала интеграл момента ударной силы относительно неподвижной точки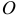 
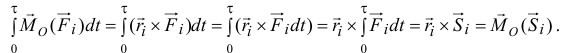
При этом предполагалось, что за малое время удара 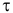радиус-вектор 
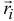считался неизменным, постоянным.
Проектируя результат этого векторного равенства на ось вращения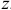 
, проходящую через точку 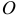, получим
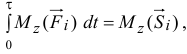
то есть интеграл равен моменту вектора импульса ударной силы относительно оси вращения. Теорема о моменте количества движения в преобразованном виде запишется теперь так:
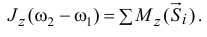
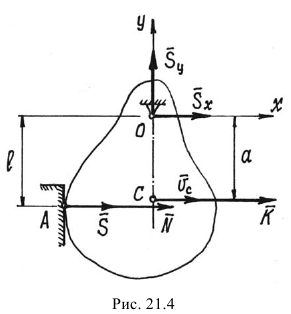
В качестве примера рассмотрим удар вращающегося тела о неподвижную преграду. Тело, вращаясь вокруг горизонтальной оси 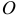, ударяется о преграду 
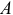(рис. 21.4). Определим ударные импульсы сил, возникающих в подшипниках на ос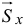и, 
и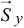 
.
По теореме об изменении количества движения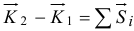 
в проекциях на ос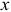и 
и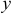 
получим два уравнения
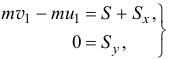
где скорости центра масс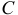 
в начале и конце удара:
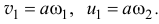
Поэтому первое уравнение станет таким:
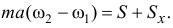
Третье уравнение по формуле (21.10) получится в виде
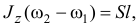
из которого находим
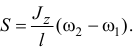
И так как коэффициент восстановления
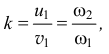
то
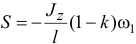
( в нашем примере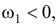 
поэтому ударный импульс 
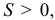направлен так, как показано на рис. 21.4).
Находим импульсы реакции оси:
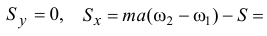
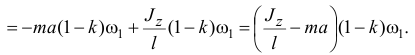
Обязательно надо обратить внимание на то, что при
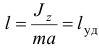
ударные импульсы в подшипниках оси будут равны нулю.
Место, точка удара, расположенная на этом расстоянии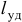 
от оси вращения, называется центром удара. При ударе по телу в этом месте ударные силы в подшипниках возникают. Кстати, заметим, что центр удара совпадает с точкой, где приложены равнодействующая сил инерции (16.1) и вектор количества движения (см. формулу (19.14а)).
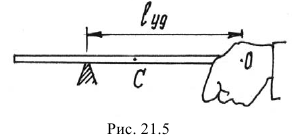
Вспомним, что при ударе длинной палкой по неподвижному предмету мы нередко испытывали рукой неприятный ударный импульс, как говорят «отбивали руку». Нетрудно найти в этом случае центр удара — место, которым следует ударить, чтобы не почувствовать это неприятное ощущение (рис. 21.5).
Так как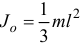 
(
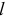— длина палки) и 
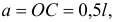то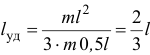 
.
Следовательно, центр удара находится на расстоянии трети длины от конца палки. Понятие центра удара учитывают при создании различных ударных механизмов и других конструкций, где встречаются ударные процессы.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Удар в теоретической механике |
| Прямой центральный удар двух тел |
| Ответы на вопросы по теоретической механике |
| Основные определения и понятия о статике |
