Силы инерции твердого тела

Силы инерции твердого тела

Главный вектор сил инерции точек тела

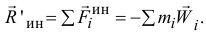
Но из определения радиуса-вектора центра масс

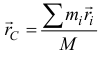
следует

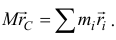
Взяв вторую производную по времени, получим

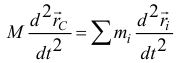
или

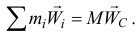
Поэтому главный вектор сил инерции точек тела при любом его движении

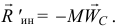
То есть модуль главного вектора равен произведению массы тела на ускорение его центра масс 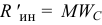и направлен вектор 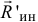в сторону, противоположную вектору ускорения центра масс.

Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, то есть он не зависит от выбора этой точки.

С определением главного момента сил инерции возникает немало сложностей. Рассмотрим несколько частных случаев.

Твердое тело движется поступательно

При таком движении главный момент сил инерции можно не определять, а находить сразу равнодействующую этих сил. Как известно, она равна главному вектору

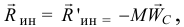
но имеет определенную точку приложения.

Поскольку при поступательном движении все точки тела имеют равные и параллельные векторы ускорений 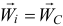то силы инерции их также будут параллельными и направленными в одну сторону. Но равнодействующая таких параллельных сил приложена к точке, радиус-вектор которой

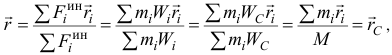
равен радиусу-вектору центра масс.

Следовательно, равнодействующая сил инерции точек тела при поступательном движении приложена к центру масс тела как к центру параллельных сил.

Твердое тело вращается вокруг неподвижной оси

Пусть тело вращается вокруг неподвижной оси 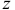(рис. 16.1).

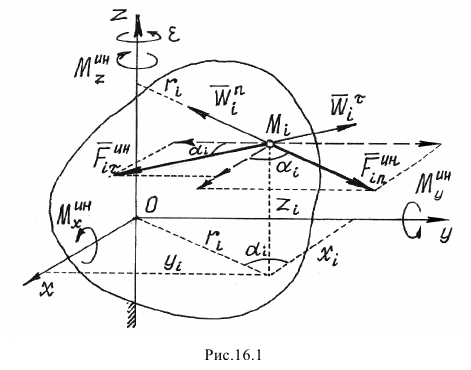
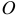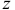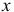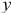Проведем в теле, в какой-нибудь точке на оси , еще две оси и , перпендикулярные друг другу, и оси z, которые вращаются вместе с телом.

Определим касательное и нормальное ускорения некоторой точки :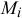

и соответствующие им силы инерции

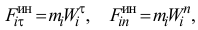
направленные противоположно ускорениям. Тогда главный момент сил инерции всех точек тела относительно оси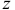

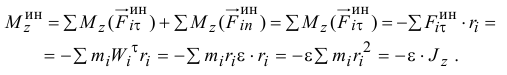
Итак, главный момент сил инерции точек тела относительно неподвижной оси вращения равен произведению момента инерции тела относительно этой оси на модуль углового ускорения

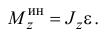
Направляется он в сторону, противоположную угловому ускорению.

Главный момент сил инерции точек тела относительно оси 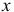, раскладывая силы инерции на две составляющие, параллельные и перпендикулярные оси 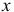(см. рис. 16.1), получается таким:

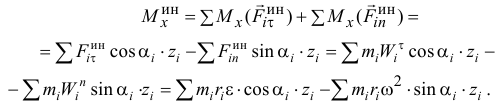
А так как

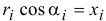
и

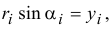
то

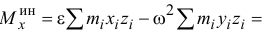
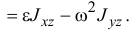
Итак, главный момент сил инерции относительно оси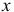

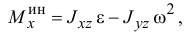
где 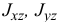— центробежные моменты инерции тела относительно соответствующих осей в точке 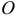(см. XIV, §2).

В частности, если тело имеет плоскость материальной симметрии, перпендикулярную оси вращения 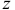, то эта ось 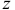будет главной осью инерции

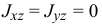
и тогда

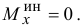
Осталось вычислить главный момент сил инерции относительно оси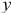

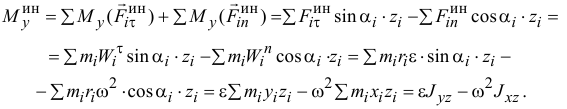
Следовательно, главный момент сил инерции точек тела относительно оси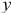

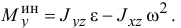
Опять, если тело имеет плоскость симметрии, перпендикулярную оси вращения, этот момент .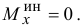

Примечания

а) Определив главные моменты сил инерции точек тела относительно взаимно перпендикулярных осей 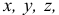, можно найти главный момент относительно точки 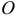, начала координат,

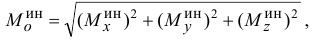
так как главные моменты относительно осей 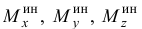являются проекциями вектора 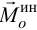на оси.

б) Если у тела имеется плоскость материальной симметрии, перпендикулярная оси вращения 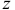, то нетрудно отыскать равнодействующую сил инерции точек тела .

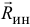Она будет расположена в этой плоскости и равна главному вектору

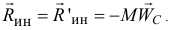
Центр масс также находится в этой плоскости.

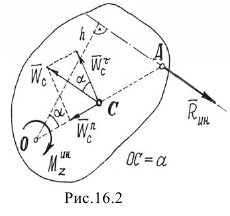
На рис. 16.2 дано сечение тела плоскостью симметрии (точка 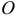— точка пересечения оси вращения 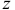и этой плоскости) и показаны центр масс 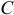, ускорение центра масс 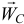и направление вектора равнодействующей .

Легко находится расстояние 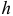от оси 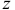, от точки 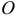, до линии действия равнодействующей

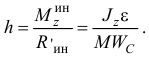
Но лучше найти расстояние 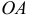от оси до линии действия равнодействующей, проведенное через центр масс :

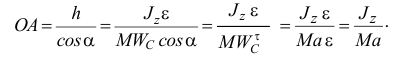
Это расстояние удобнее тем, что оно не зависит от закона вращения тела, определяется только его геометрией. Следовательно, в этом случае у тела имеется такая точка 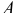, к которой всегда приложена равнодействующая сил инерции точек тела (направление линии действия вектора , конечно, может быть различным, зависящим от закона вращения, но параллельным вектору ускорения ).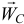

Тело совершает плоскопараллельное движение

При плоскопараллельном движении ускорение точки тела есть сумма трех ускорений: ускорения полюса, нормального ускорения и касательного ускорения точки при вращении вокруг полюса. Если полюс — центр масс 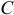, то ускорение 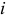-й точки 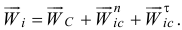Соответственно у точки будут три составляющие силы инерции: 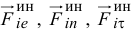(рис. 16.3).

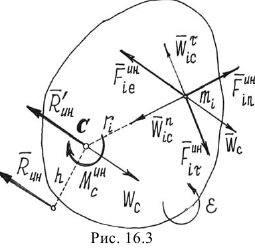
Тогда главный момент сил инерции точек тела относительно оси 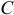, проходящей через центр масс перпендикулярно плоскости движения,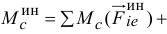

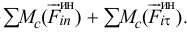
Но первая сумма равна нулю, так как по теореме Вариньона она равна моменту равнодействующей сил 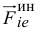, которая приложена к центру масс, потому что переносное движение тела при плоскопараллельном движении — поступательное.

Вторая сумма также равна нулю, так как линии действия этих сил 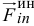пересекают ось 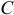. Поэтому

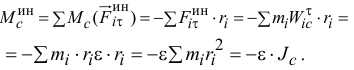
Итак, главный момент сил инерции точек тела при плоскопараллельном движении относительно центральной оси 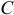, перпендикулярной плоскости движения, равен произведению момента инерции относительно этой оси на модуль углового ускорения

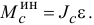
Направляется этот момент в сторону, противоположную направлению углового ускорения .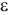

При желании можно найти равнодействующую сил инерции. Она будет равна главному вектору

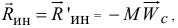
параллельна ему, а линия действия ее будет находиться на расстоянии

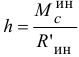
от центра масс, отложенном перпендикулярно 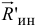в сторону, определяемую направлением момента 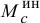(см. рис. 16.3).

Принцип Даламбера удобно использовать при решении задач, в которых требуется определить неизвестные силы и иногда ускорение.

Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:

Помощь по теоретической механике

Кстати возможно вам будут полезны эти страницы:

Закон сохранения энергии

Принцип Даламбера

Возможные перемещения. Классификация связей

Принцип возможных перемещений при равновесии материальной системы