Моменты инерции тел

Моменты инерции тел

Инерционные свойства твердого тела характеризуются не только его массой 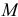, определяющей инерционность при поступательном движении, но и моментом инерции, определяющим инерционность вращательного движения тела.

Моментом инерции тела относительно оси называется сумма произведений массы каждой точки на квадрат расстояния от точки до оси

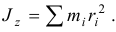
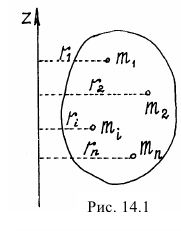
Заметим сразу, что момент инерции тела — это геометрическая характеристика тела, не зависящая от его движения (рис. 14.1).

Для однородных тел простой симметричной формы момент инерции можно найти в справочниках. А моменты инерции некоторых тел, которые чаще всего встречаются при исследовании движения материальных систем, даны на рис. 14.2.

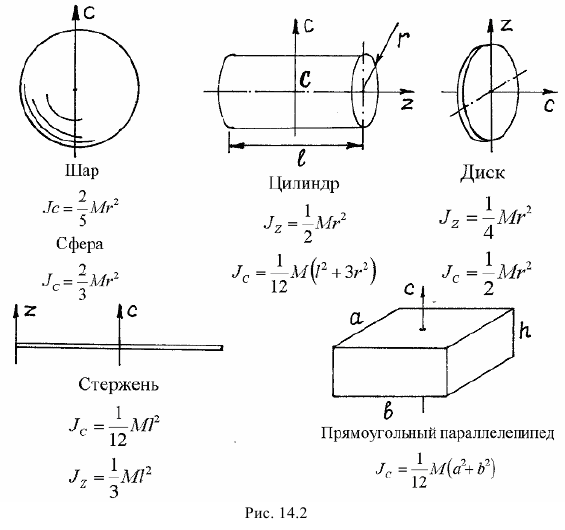
На рисунке даны моменты инерции тел относительно осей симметрии. Но нередко при исследовании движения реальных механизмов приходится определять моменты инерции относительно осей, не совпадающих с осями симметрии. Этому помогают следующие теоремы.

Теорема Гюйгенса-Штейнера о моментах инерции тела относительно параллельных осей

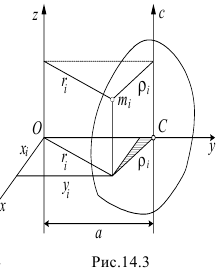
Найдем зависимость между моментами инерции тела относительно параллельных осе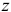й и 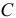(рис. 14.3). Ось 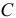, проходящая через центр масс тела, называется центральной осью. Расстояние между осями — .

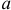По определению (14.3)

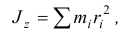
причем

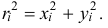
Но из заштрихованного прямоугольного треугольника (см. рис. 14.3) следует, что

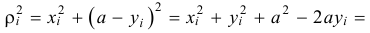
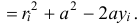
Значит

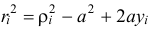
и момент инерции относительно оси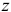

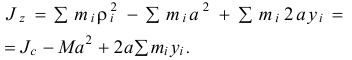
Но по формуле (14.2) сумма

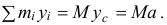
Поэтому

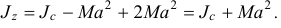
Следовательно, момент инерции тела относительно оси 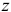равен сумме момента инерции тела относительно центральной оси 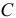, параллельной оси 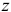, и произведения массы тела на квадрат расстояния между осями

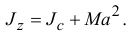
Так, например, момент инерции стержня относительно оси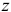

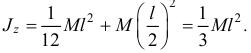
А момент инерции прямоугольного параллелепипеда относительно оси 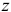, проведенной по какому-нибудь вертикальному ребру

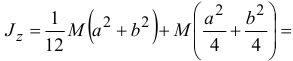
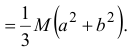
Момент инерции тела относительно произвольной оси

Найдем момент инерции тела относительно оси 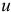, проходящей через некоторую точку 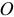(рис. 14.4).

По определению момент инерции

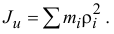
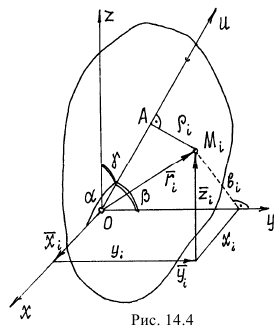
Поместим в точку 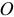начало координатных осей 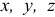. Из прямоугольного треугольника 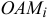следует

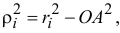
где

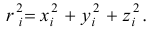
И так как радиус-вектор точки 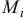равен

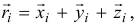
то, проектируя это равенство на ось 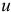, получим

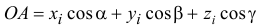
Как известно из тригонометрии

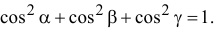
Поэтому

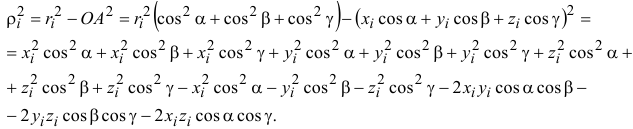
И, группируя подобные члены, содержащие косинусы одинаковых углов,

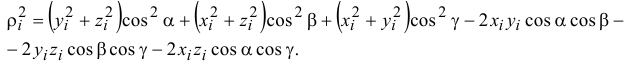
Но

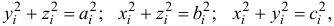
где

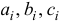
расстояние от точки 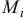до осей 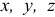соответственно. Поэтому

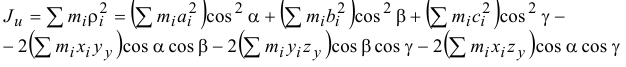
или

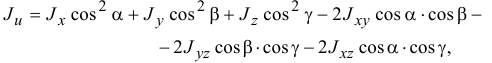
где 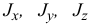— моменты инерции тела относительно осей координат; 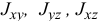— центробежные моменты инерции относительно осей, отмеченных в индексах.

Если два центробежных момента инерции, оба содержащих в индексах названия какой-нибудь одной оси, равны нулю, то эта ось называется

главной осью инерции. Например, есл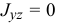и и 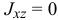, то ось 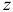— главная ось инерции.

Так как все моменты инерции зависят от того, где находится точка 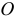, от выбора начала координат, то обязательно надо указать, для какой точки определены эти моменты инерции. Если начало координат взято в центре масс 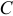, то все главные оси инерции называются главными центральными осями инерции.

Если в данной точке координатные оси являются главными осями инерции (центробежные моменты инерции относительно их равны нулю), то формула (14.5) упрощается

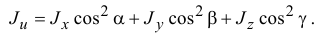
Иногда по некоторым признакам нетрудно найти главные оси инерции тела.

• Если у однородного тела имеется ось симметрии, то эта ось является главной центральной осью инерции.

Действительно. Направим координатную ось 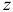по оси симметрии. Тогда для каждой точки тела с координатами 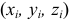можно отыскать точку с координатами 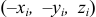и поэтому центробежные моменты инерци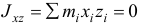и и 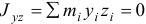. Значит ось 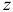— главная ось инерции и центральная ось, так как центр масс, как известно, находится на оси симметрии. Причем, эта ось будет главной для любой точки, расположенной на оси симметрии.

• Если у однородного тела имеется плоскость симметрии, то любая ось, перпендикулярная ей, будет главной осью инерции для всех точек этой плоскости.

Направим ось 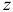перпендикулярно плоскости симметрии из любой ее точки 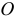, назначив там начало координат. Тогда для каждой точки тела с координатами 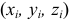можно найти симметричную ей точку с координатами 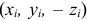. Поэтому центробежные моменты инерци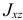и и 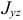будут равны нулю. Значит ось 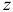— главная ось инерции.

Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:

Помощь по теоретической механике

Кстати возможно вам будут полезны эти страницы:

Относительное движение материальной точки

Основные определения и характеристики материальной системы

Работа силы в материальной системы

Потенциальная энергия