Энтропия и вероятность.

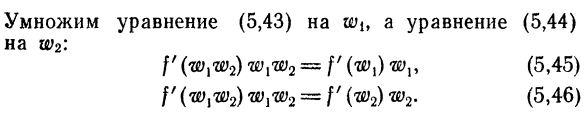
Энтропия и вероятность.

• Энтропия и вероятность Вернемся к заключительному рассмотрению Термодинамическая система. Необратимый Процесс такой системы включает в себя- Увеличение энтропии. Его максимальное значение равно Равновесное состояние системы Может быть. Таким образом, статистическая причина увеличения Энтропия необратимого процесса должна возрастать

 В этом случае вероятность состояния системы. Так… Энтропия системы является специфической вероятностной функцией Ее состояние. Это главное, что нужно решить Сущность второго закона термодинамики и установлена Впервые установлена связь между энтропией и вероятностью Его представлял Больцман. Найдите тип зависимости Где W-вероятность состояния.

Это главное, что нужно решить Сущность второго закона термодинамики и установлена Людмила Фирмаль

Энтропия и вероятности двух систем показаны следующим образом Вероятности с Si, W \и S2, w2i и энтропией соответственно Сложная система, состоящая из первых 2 S и W. Затем, основываясь на предложении Больцмана、 Возникают зависимости： С= / К), Е 39） С2 * = ф(ш&е, 40） Ы = ф(ш). Е, 41） Предполагая, что энтропия системы имеет характеристику Аддитивность, то есть энтропия системы равна сумме энтропии

Энтропиядля отдельных частей и вероятность для состояний Сложная система равна произведению вероятности Состояние отдельной системы мы пишем： Или С-ф (ш {) + Ф (В2) = Ф(wxw2). Е, 42） Относительно W\ мы сначала дифференцируем это уравнение、 И по w2i вы получаете Ф /(wlw2) Да2 ^ ФФ(ш {), е, 43） Е, 44） Формула E, 43) умножается на w, Формула E, 44 Да2.： Ф(ж, а> 2)^®1Щ-в (^Я) гор е, 45） ФФ (wlw2) ш ^ = Ф(В2) Е, 46)отсюда Р (У) У ^(р(у) у, 47）

• Иначе говоря P(Вт) Вт = const и = К Е, 48） Между тем, из отношения е, 41） Г(•)=?•<5 ′ 49> Эквивалентность е, 48) и Е, 49) ДС к — j — = — износ, и путем его интегрирования ： S = k в w + const E, 50） Соотношение Е, 50) указывает на пропорциональность* Энтропия системы-это логарифм стохастического состояния、 Это Ниджа system. As дополнительный анализ показывает Формула E, 50), коэффициент

Написание выражения энтропии через вероятности Статус Людмила Фирмаль

пропорциональности k Эта формула имеет постоянную Больцмана. Основываясь на приведенных выше рассуждениях、 Больцман дал эту формулировку второму закону* модиннамки: «природа стремится меньше искать от государств» Скорее всего, это будут более вероятные условия.」

Смотрите также:

Решение задач по термодинамике

Энтропия и равновесие системы.	0 так называемой «тепловой смерти» вселенной.
Статистический характер второго начала термодинамики.	Термодинамика и проблемы излучения