Оглавление:
Способы задания движения точки
Прежде чем заняться исследованием движения точки, определением характеристик этого движения, надо научиться определять положение точки в пространстве в нужный момент времени.
Для этого существует несколько способов задания движения.
Естественный способ
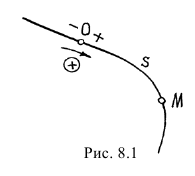
Чтобы определить движение точки естественным способом, должны быть заранее заданы (рис.8.1) траектория движения точки (линия, по которой точка движется); начало отсчёта (точка 
, от которой по траектории отсчитывается расстояние 
до движущейся точки 
); направление, в котором откладываются положительные значения характеристик движения (указывается стрелкой либо знаками + и -); закон движения 
.
Пример:
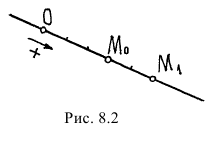
Точка движется по прямой линии, по закону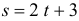 
(см) (рис. 8.2).
В начале движения при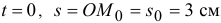 
. Положение точки 
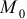называется начальным положением. При 
.
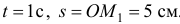Конечно, за 1с точка прошла расстояние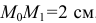 
. Так что — это не путь, пройденный точкой, а расстояние от начала отсчёта до точки.
Координатный способ
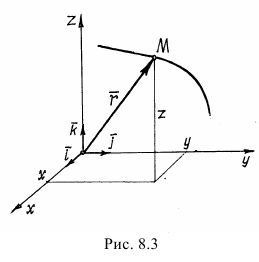
Этим способом положение точки в какой-либо системе координат определяется её координатами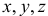 
(рис. 8.3). При движении точки эти координаты изменяются. Поэтому, чтобы определить положение точки в нужный момент времени, должны быть заданы координаты как функции времени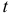 
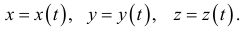
Эти функции называются уравнениями движения точки.
Уравнения движения позволяют определить не только положение точки в любой момент времени, но и все характеристики движения, в том числе и траекторию движения.
Чтобы получить уравнение траектории, надо из уравнений движения исключить параметр .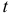
Пример:
Движение точки задано уравнениями (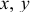
— в сантиметрах, 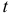— в секундах)
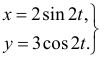
Чтобы исключить время, параметр 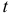найдём из первого уравнения
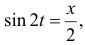
из второго
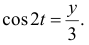
Затем возведем их в квадрат и сложим. Так как
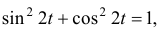
получим
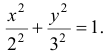
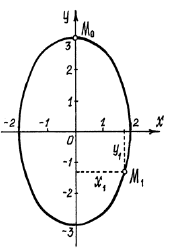
Это уравнение эллипса с полуосями 2 см и 3 см (рис. 8.4).
Начальное положение точк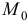и 
(при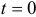 
) определяется координатами 
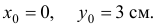Через 1с точка будет в положении 
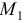с координатами
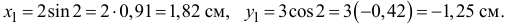
Примечание
Движение точки может быть задано с помощью и других координат, например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости с заданием движения цилиндрическими и сферическими координатами можно ознакомиться по учебникам.
Векторный способ
Положение точки можно определить заданием вектора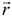 
, проведённого из неподвижной точки 
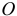, предполагая, что точка 
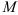находится на конце этого вектора (см. рис. 8.3). Этот вектор называется радиусом-вектором точки 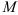. Конечно, чтобы определить положение точки в любой момент времени, радиус-вектор должен быть задан как функция времени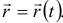 
Нетрудно установить зависимость между векторным и координатным способами задания движения.
Разложим вектор 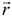на составляющие по осям координат:
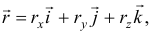где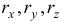 
— проекции вектора на оси; 
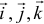— единичные векторы, направленные по осям, орты осей. Так как начало 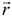вектора находится в начале координат, то проекции вектора будут равны координатам точки 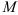. Поэтому
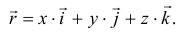
Траектория движения точки — это линия, которую описывает конец изменяющегося радиуса-вектора. Эта линия называется годографом вектора .
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Трение скольжения |
| Трение качения |
| Скорость точки |
| Ускорение точки |
