Сложение параллельных сил. Центр параллельных сил
Пусть даны две параллельные силы 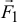 и
и 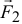 , направленные в одну сторону и приложенные к точкам
, направленные в одну сторону и приложенные к точкам 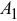 и
и 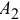 (рис. 6.1).
(рис. 6.1).
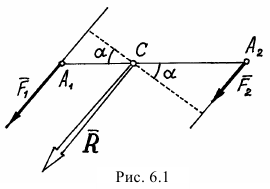
Конечно величина их равнодействующей
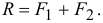
Вектор ее параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона (5.8) найдем точку приложения равнодействующей — точку 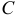 . По этой теореме
. По этой теореме
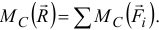
Значит,
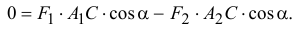
Отсюда
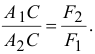
То есть точка приложения равнодействующей делит расстояние между точками 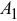 и
и 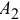 на части, обратно пропорциональные силам.
на части, обратно пропорциональные силам.
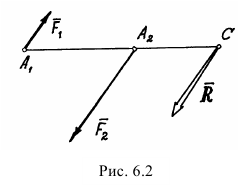
Если параллельные силы направлены в противоположные стороны (рис. 6.2), то аналогично можно доказать, что равнодействующая по величине будет равна разности сил: 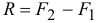 (если
(если 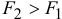 ), параллельна им, направлена в сторону большей силы и расположена за большей силой — в точке
), параллельна им, направлена в сторону большей силы и расположена за большей силой — в точке 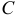 . А расстояния от точки
. А расстояния от точки 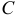 до точек приложения сил обратно пропорциональны силам:
до точек приложения сил обратно пропорциональны силам:
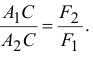
Следует заметить, что если точка приложения равнодействующей расположена на одной прямой с точками 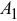 и
и 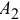 , точками приложения сил, то при повороте этих сил в одном направлении на одинаковый угол равнодействующая также повернется вокруг точки приложения
, точками приложения сил, то при повороте этих сил в одном направлении на одинаковый угол равнодействующая также повернется вокруг точки приложения 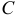 в том же направлении и останется параллельной им.
в том же направлении и останется параллельной им.
Такая точка приложения равнодействующей называется центром параллельных сил.
Конечно, если хотя бы одну из сил перенести по своей линии действия в другую точку, то и точка приложения равнодействующей, центр параллельных сил, тоже переместится по линии действия.
Следовательно, положение центра параллельных сил зависит от координат точек приложения сил.
Центром нескольких параллельных сил, найденным последовательным сложением каждых двух сил, будем называть точку 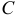 , радиус-вектор которой определяется формулой
, радиус-вектор которой определяется формулой
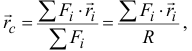
где 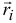 — радиусы-векторы точек приложения сил;
— радиусы-векторы точек приложения сил; 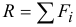 — величина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).
— величина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).
Используя равенство (6.1), нетрудно найти координаты центра параллельных сил. Если радиусы-векторы откладывать из начала координат, то проекции радиусов-векторов точек на оси будут равны координатам этих точек. Поэтому, проектируя векторное равенство (6.1) на оси, получим
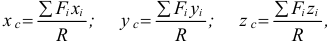
где 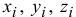 — координаты точек приложения сил.
— координаты точек приложения сил.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Пара сил. Момент, свойства, сложение пары сил |
| Приведение силы к точке |
| Центр тяжести тел |
| Распределённые силы |
