Оглавление:
Распределение скоростей точек плоской фигуры
Принимая мгновенный центр 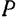 скоростей фигуры за полюс и имея в виду, что скорость этой точки в рассматриваемый момент равна нулю, легко найти скорости всех остальных точек фигуры в этот же момент времени:
скоростей фигуры за полюс и имея в виду, что скорость этой точки в рассматриваемый момент равна нулю, легко найти скорости всех остальных точек фигуры в этот же момент времени:
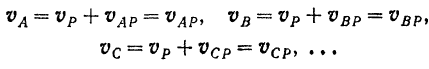
Следовательно, скорость любой точки плоской фигуры равна скорости этой точки вокруг мгновенного центра скоростей фигуры.
Исходя из этого, легко найти модуль и направление скорости каждой точки фигуры (если положение мгновенного центра и угловая скорость фигуры, не зависящая от выбора полюса, для данного момента времени известны):
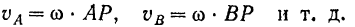
Деля почленно обе части последних равенств, находим
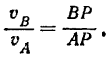
Модули скоростей раз личных точек фигуры в каждый момент пропорциональны расстояниям этих точек от соответствующего данному моменту мгновенного центра скоростей фигуры. Направлены же скорости различных точек фигуры, перпендикулярно к отрезкам, соединяющим соответствующие точки с мгновенным центром скоростей, в сторону вращения фигуры (рис. 151).
Таким образом, скорости различных точек плоской фигуры в любой момент времени распределяются так, как если бы фигура вращалась в этот момент времени вокруг мгновенного центра скоростей, занимающего в разные моменты различные положения как относительно движущейся фигуры, так и относительно неподвижной плоскости, в которой движется фигура.
При плоском движении тела скорости его точек в каждый данный момент времени распределяются так, как будто бы тело вращается в этот момент вокруг некоторой, так называемой мгновенной оси вращения, проходящей через соответствующий данному моменту мгновенный центр скоростей фигуры и перпендикулярной к ее плоскости. Это следует из того, что при плоском движении тела все его точки, лежащие на одном пер-пендик>ляре к неподвижной плоскости, движутся одинаково. Поэтому все точки тела, лежащие на мгновенной оси вращения, т.е. на прямой, проходящей через мгновенный аенгр скоростей фигуры и перпендикулярной к ее плоскости, будут в данный момент иметь скорость, равную нулю, а все точки тела, лежащие на перпендикуляре к плоскости фигуры, восставленном в какой-либо другой ее точке, будут иметь такие же скорости, как соответствующая точка фигуры.
Каждому моменту времени соответствует свое положение мгновенного центра скоростей и свое положение мгновенной осп. На это обстоятельство и указывают сами их названия: «мгновенный» центр и «мгновенная» ось.
Заметим, что нельзя полностью отождествлять вращение тела вокруг мгновенной оси в данный момент с вращением тела вокруг неподвижной оси. В последнем случае скорости всех точек тела, лежащих на оси, равны нулю все время движения тела и потому их ускорения равны нулю. Точки же тела, совпадающие в данный момент времени с мгновенной осью вращения, имеют скорости, равные нулю только в этот момент, и движутся с ускорением.
Можно доказать, что при непоступательном движении плоской фигуры в се плоскости всегда есть такая, неизменно связанная с фигурой, точка, ускорение которой в данный момент времени равно нулю. Ускорения различных точек плоской фигуры в каждый момент распределяются так, как если бы фигура вращалась в этот момент вокруг этой точки, называемой мгновенным центром ускорений.
Но положения мгновенного центра скоростей и мгновенного центра ускорений не совпадают. Так, например, при равномерном качении колеса по неподвижному прямолинейному рельсу мгновенный центр ускорений колеса лежит в центре колеса — точке 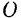 (рис. 154). Эта точка
(рис. 154). Эта точка
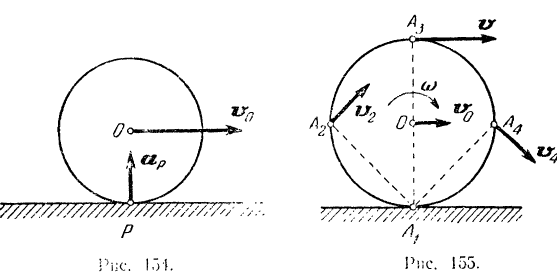
движется прямолинейно и равномерно со скоростью 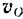 и ее ускорение равно нулю. Мгновенный же центр скоростей колеса лежит, как известно, в точке
и ее ускорение равно нулю. Мгновенный же центр скоростей колеса лежит, как известно, в точке 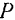 касания колеса с рельсом. Его скорость в данный момент равна нулю, ускорение же
касания колеса с рельсом. Его скорость в данный момент равна нулю, ускорение же 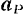 этой точки
этой точки 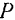 равно ее нормальному ускорению
равно ее нормальному ускорению 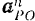 во вращательном движении вокруг точки
во вращательном движении вокруг точки 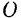 .
.
Положение центра ускорений совпадает с положенном центра скоростей лишь при вращении тела вокруг неподвижной оси.
Пример задачи:
Цилиндр, лежащий на горизонтальной плоскости, обмотан веревкой, один конец которой прикреплен к цилиндру, а другой свободен. Найти угловую скорость 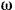 цилиндра, скорость
цилиндра, скорость 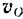 его центр
его центр 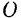 и скорость концов
и скорость концов 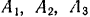 и
и 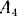 вертикального и горизонтального диаметров перпендикулярного сечения цилиндра. Свободный конец веревки тянут параллельно плоскости и перпендикулярно к оси цилиндра с постоянной скоростью
вертикального и горизонтального диаметров перпендикулярного сечения цилиндра. Свободный конец веревки тянут параллельно плоскости и перпендикулярно к оси цилиндра с постоянной скоростью 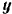 (рис. 155). Цилиндр катится без скольжения. Радиус цилиндра равен
(рис. 155). Цилиндр катится без скольжения. Радиус цилиндра равен 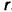 .
.
Решение:
Проведем через веревку плоскость, перпендикулярную к оси цилиндра. В сечении получится круг, катящийся по горизонтальной прямой. Так как этот круг катится без скольжения, го скорость точки 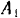 и в которой он касается прямой, равна нулю, следовательно, эта точка является мгновенным центром скоростей круга. Скорость точки
и в которой он касается прямой, равна нулю, следовательно, эта точка является мгновенным центром скоростей круга. Скорость точки 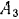 круга, в которой его касается свободный конец веревки, равна скорости
круга, в которой его касается свободный конец веревки, равна скорости 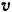 , с которой тянут веревку. Зная положение мгновенного центра скоростей круга и скорость его одной точки
, с которой тянут веревку. Зная положение мгновенного центра скоростей круга и скорость его одной точки 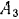 , находим угловую скорость цилиндра и скорости точек
, находим угловую скорость цилиндра и скорости точек 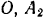 и
и 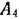 :
:
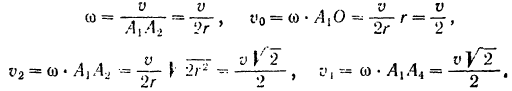
Направления векторов 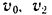 и
и 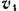 показаны на рис. 158.
показаны на рис. 158.
Пример задачи:
Определить скорость ползуна 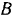 и средней точки
и средней точки 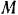 шатуна
шатуна 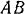 кривошипно-шатунного механизма (рис. 156. о) в момент, когда кривошип
кривошипно-шатунного механизма (рис. 156. о) в момент, когда кривошип 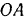 составляет с линией
составляет с линией 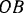 движения ползуна угол
движения ползуна угол 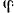 . Вычислить, в частности, скорости этих точек для двух положений механизма, когда
. Вычислить, в частности, скорости этих точек для двух положений механизма, когда 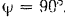 и
и 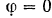 , полагая
, полагая 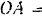
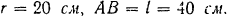 . Угловая скорость кривошипа постоянна и равна
. Угловая скорость кривошипа постоянна и равна 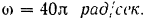 . Направление его вращения показано на рисунки.
. Направление его вращения показано на рисунки.
Решение:
Направления скоростей двух точек 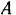 и
и 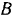 шатуна нам всегда известны. Точка
шатуна нам всегда известны. Точка 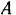 есть точка шатуна
есть точка шатуна 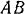 , общая с кривошипом
, общая с кривошипом 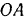 . Но кривошип совершает вращательное движение, и потому его точка
. Но кривошип совершает вращательное движение, и потому его точка 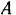 движется по окружности радиуса
движется по окружности радиуса 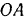 и, следовательно, скорость
и, следовательно, скорость 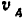 этой точки перпендикулярна к радиусу
этой точки перпендикулярна к радиусу 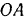 .
.
Точка 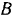 есть точка шатуна, общая с ползуном
есть точка шатуна, общая с ползуном 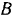 . Но ползун может двигаться только поступательно вдоль своих направляющих и, следовательно, скорость точки
. Но ползун может двигаться только поступательно вдоль своих направляющих и, следовательно, скорость точки 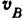 направлена по линии движения
направлена по линии движения 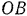 ползуна. Зная же для данного момента направления скоростей двух точек шатуна, легко найти и положение его мгновенного центра скоростей. Эта точка
ползуна. Зная же для данного момента направления скоростей двух точек шатуна, легко найти и положение его мгновенного центра скоростей. Эта точка 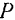 лежит на пересечении перпендикуляров, воспаленных в двух точках
лежит на пересечении перпендикуляров, воспаленных в двух точках 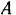 и
и 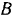 шатуна к направлением скоростей vrnx точек (рис. 156, а). Угловая скорость шатуна равна
шатуна к направлением скоростей vrnx точек (рис. 156, а). Угловая скорость шатуна равна
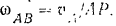
модуль скорости точки 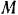 шатуна
шатуна
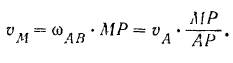
Модуль скорости ползуна (точки 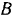 шатуна)
шатуна)
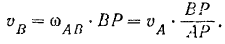
Направлены скорости этих точек перпендикулярно соответственно к отрезкам 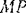 и
и 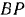 в сторону вращения шатуна (так, как изображено на рис. 156, а). Величину скорости точки
в сторону вращения шатуна (так, как изображено на рис. 156, а). Величину скорости точки 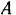 легко вычислить по формуле
легко вычислить по формуле
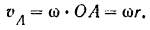
Зная для данного момента угол 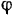 , всегда можно найти и длины
, всегда можно найти и длины 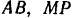 и
и 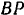 или вычислением (решая соответствующие треугольники), или графически (строя схему механизма в масштабе, по заданным размерам его звеньев и углу
или вычислением (решая соответствующие треугольники), или графически (строя схему механизма в масштабе, по заданным размерам его звеньев и углу 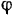 ).
).
Решим теперь ту же задачу для частных случаев, когда 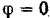 и
и 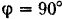 . Расположение звеньев механизма и направление скорости
. Расположение звеньев механизма и направление скорости
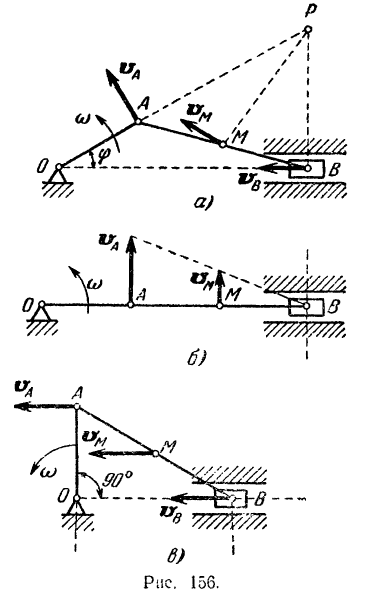
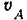 точки
точки 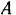 при угле поворота кривошипа
при угле поворота кривошипа 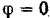 показано на рис. 156,6. Скорость точки
показано на рис. 156,6. Скорость точки 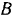 во всех случаях может быть направлена лишь по линии движения ползуна. Мгновенным центром шатуна
во всех случаях может быть направлена лишь по линии движения ползуна. Мгновенным центром шатуна 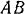 будет точка
будет точка 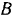 , так как в ней в данном случае пересекаются перпендикуляры, восставленные в точках
, так как в ней в данном случае пересекаются перпендикуляры, восставленные в точках 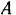 и
и 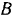 к скоростям этих точек. Так как точка
к скоростям этих точек. Так как точка 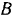 совпадает в данный момент с мгновенным центром, то скорость этой точки (скорость ползуна) равна нулю (механизм находится в «мертвом» положении). Угловая скорость шатуна
совпадает в данный момент с мгновенным центром, то скорость этой точки (скорость ползуна) равна нулю (механизм находится в «мертвом» положении). Угловая скорость шатуна
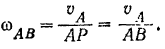
Скорость точки 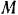 шатуна
шатуна
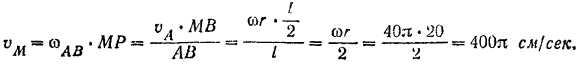
Расположение механизма и направленна скоростей 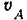 и
и 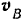 при угле поворота кривошипа
при угле поворота кривошипа 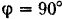 показано на рис. 156, е. Так как скорости
показано на рис. 156, е. Так как скорости 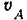 и
и 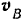 параллельны и точки
параллельны и точки 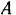 и
и 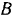 не лежат на одном перпендикуляре к направлениям этих скоростей, то в данный момент мгновенный центр скоростей шатуна
не лежат на одном перпендикуляре к направлениям этих скоростей, то в данный момент мгновенный центр скоростей шатуна 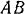 лежит в бесконечности, его угловая скорость
лежит в бесконечности, его угловая скорость
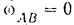
и он совершает мгновенное поступательное движение. Следовательно, в данный момент
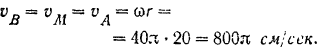
Пример задачи:
Две параллельные рейки движутся в разные стороны с постоянными скоростями 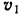 и
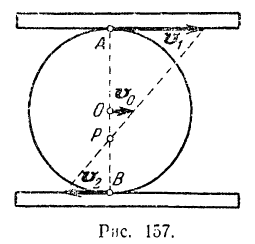
и 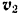 (рис. 157). Между рейками зажат диск радиусом
(рис. 157). Между рейками зажат диск радиусом 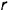 , катящийся по рейкам без скольжения. Найти угловую скорость диска и скорость его центра
, катящийся по рейкам без скольжения. Найти угловую скорость диска и скорость его центра 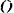 , если
, если 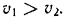 .
.
Решение:
Так как диск катится по рейкам без скольжения, то скорость его точки 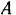 , в которой диск соприкасается с верхней рейкой, равна скорости этой рейки
, в которой диск соприкасается с верхней рейкой, равна скорости этой рейки 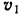 . На том же основании скорость точки
. На том же основании скорость точки 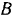 диска равна скорости нижней рейки
диска равна скорости нижней рейки 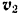 . Так как скорости двух точек
. Так как скорости двух точек 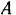 и
и 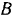 диска параллельны, а сами точки лежат на одном перпендикуляре к скоростям этих точек, то мгновенный центр
диска параллельны, а сами точки лежат на одном перпендикуляре к скоростям этих точек, то мгновенный центр 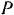 скоростей диска определится из пропорции:
скоростей диска определится из пропорции:
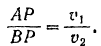
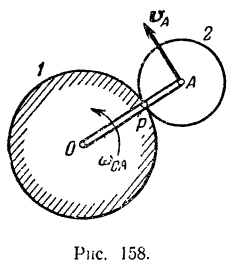
С другой стороны,
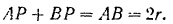
Решая эти два уравнения совместно, находим
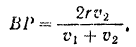
Угловая скорость диска
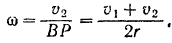
Расстояние центра 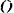 диска от мгновенного центра скоростей
диска от мгновенного центра скоростей
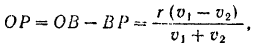
Скорость центра диска
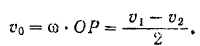
Пример задачи:
Кривошип 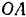 (рис. 158), вращаясь с угловой скоростью
(рис. 158), вращаясь с угловой скоростью 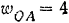 paд/сек вокруг оси неподвижного колеса радиуса
paд/сек вокруг оси неподвижного колеса радиуса 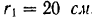 , приводит во вращение свободно насаженное на его конце
, приводит во вращение свободно насаженное на его конце 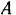 колесо 2 радиуса
колесо 2 радиуса 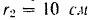 . Определить угловую скорость колеса 2.
. Определить угловую скорость колеса 2.
Решение:
Сателлит, катясь без скольжения по неподвижному колесу 1, совершает плоское движение. Положение мгновенного центра скоростей сателлита известно. Он лежит в точке 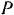 касания колеса. Следовательно, для определения угловой скорости
касания колеса. Следовательно, для определения угловой скорости 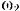 сателлита достаточно знать скорость какой-либо одной его точки. Пользуясь тем, что точка
сателлита достаточно знать скорость какой-либо одной его точки. Пользуясь тем, что точка 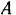 принадлежит не только сателлиту, но и кривошипу
принадлежит не только сателлиту, но и кривошипу 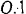 . найдем ее скорость:
. найдем ее скорость:
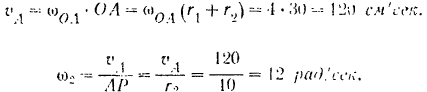
Понятие об определении ускорений точек плоской фигуры
Как мы уже знаем. всякое движение плоский фигуры 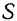 в ее плоскости можно разложить на два движения: 1) переносное поступательное движение вместе с произвольно выбранной точкой фигуры (полюсом) и относительное вращательное движение фигуры вокруг полюса.
в ее плоскости можно разложить на два движения: 1) переносное поступательное движение вместе с произвольно выбранной точкой фигуры (полюсом) и относительное вращательное движение фигуры вокруг полюса.
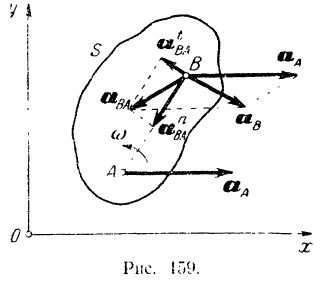
Выберем за полюс какую-либо точку 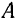 фигуры (рис. 159).
фигуры (рис. 159).
По теореме о сложении ускорений точки при переносном поступательном движении абсолютное ускорение 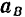 любой точки
любой точки 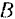 фигуры будет равно геометрической сумме ускорения
фигуры будет равно геометрической сумме ускорения 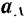 полюса
полюса 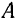 (переносного ускорения) и ускорения
(переносного ускорения) и ускорения 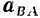 данной точки.
данной точки.
В во вращательном движении этой точки вокруг полюса (относительного ускорения):
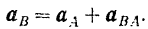
Относительное же ускорение 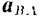 точки
точки 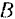 во вращательном движении вокруг полюса
во вращательном движении вокруг полюса 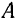 , в свою очередь, удобно представить как геометрическую сумму двух ускорений: тангенциального ускорения
, в свою очередь, удобно представить как геометрическую сумму двух ускорений: тангенциального ускорения 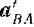 и нормального ускорения
и нормального ускорения 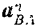 :
:
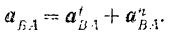
Отсюда получаем следующее выражение для ускорения точки 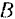 фигуры:
фигуры:
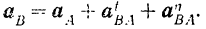
Модуль относительного тангенциального ускорения точки
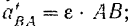
направлен же вектор 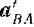 перпендикулярно к радиусу
перпендикулярно к радиусу 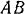 в сторону вращения фигуры (см. рис. 159) при ускоренном вращении и в противоположную сторону при замедленном.
в сторону вращения фигуры (см. рис. 159) при ускоренном вращении и в противоположную сторону при замедленном.
Модуль относительного нормального ускорения точки
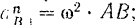
направлен сектор 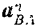 всегда к полюсу, т. е. от
всегда к полюсу, т. е. от 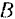 к
к 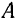 .
.
На рис. 159 показаны вектор 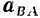 относительного ускорения точки
относительного ускорения точки 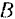 , изображаемый диагональю параллелограмма, построенного на векторах
, изображаемый диагональю параллелограмма, построенного на векторах 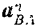 и
и 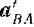 , и вектор
, и вектор 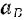 абсолютного ускорения этой точки, изображаемый диагональю параллелограмма, построенного на векторах
абсолютного ускорения этой точки, изображаемый диагональю параллелограмма, построенного на векторах 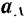 и
и 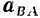 .
.
Пример задачи:
Найти угловую скорость и угловое ускорение 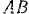 нецентрального кривошипно-шатунного механизма (рис. 160. а), а также ускорение ползуна
нецентрального кривошипно-шатунного механизма (рис. 160. а), а также ускорение ползуна 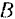 в тот момент, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной осью угол
в тот момент, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной осью угол
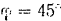
Длина кривошипа
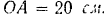
Длина шатуна
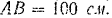
Кривошип вращается равномерно с угловой скоростью
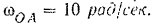
Решение:
Шатун 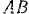 совершает плоское движение. Скорость
совершает плоское движение. Скорость 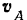 его точки
его точки 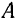 (центра шарнира, соединяющего шатун
(центра шарнира, соединяющего шатун 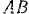 с кривошипом
с кривошипом 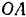 ) направлена перпендикулярно к радиусу
) направлена перпендикулярно к радиусу 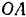 в сторону вращения кривошипа и равна по модулю
в сторону вращения кривошипа и равна по модулю
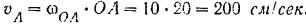
Скорость 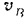 точки
точки 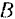 шатуна (центра шарнира, соединяющего шатун с ползуном
шатуна (центра шарнира, соединяющего шатун с ползуном 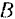 ) направлена по линии движения ползуна.
) направлена по линии движения ползуна.
Мгновенный центр 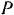 скоростей шатуна лежит на пересечении линий проведенных из точек
скоростей шатуна лежит на пересечении линий проведенных из точек 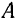 и
и 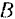 перпендикулярно к скоростям этих точек. В заданном положении механизма, как это ясно из рис. 160.
перпендикулярно к скоростям этих точек. В заданном положении механизма, как это ясно из рис. 160.
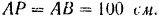
Следовательно, угловая скорость шатуна
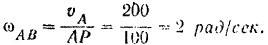
Для определения ускорении ползуна (точки 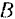 шатуна) примем за полюс точку
шатуна) примем за полюс точку 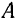 шатуна.
шатуна.
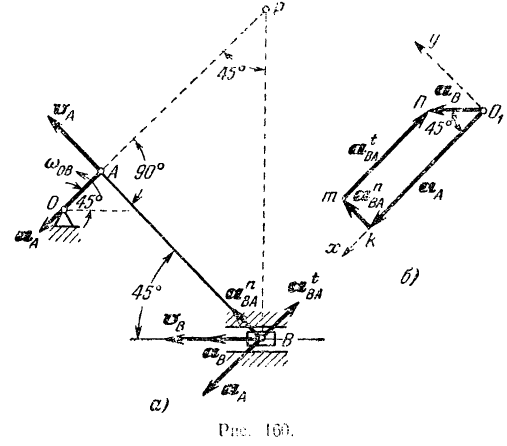
Так как кривошип вращается с постоянной угловой скоростью тангенциальное ускорение его точки
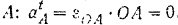
Следовательно, полное ускорение точки 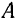 равно по модулю
равно по модулю
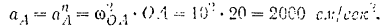
Направлен же вектор 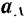 по радиусу
по радиусу 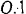 от
от 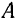 к центру
к центру 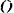 .
.
Но формуле (103) ускорения точка 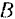 шатуна
шатуна
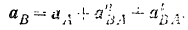
Модуль нормального ускорения 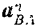 точки
точки 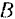 к полюсу
к полюсу 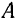 . Тангенциальное ускорение
. Тангенциальное ускорение 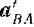 точки
точки 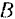 во вращательном движении вокруг полюса
во вращательном движении вокруг полюса 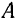 должно быть направленно перпендикулярно к
должно быть направленно перпендикулярно к 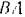 .
.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Теорема о проекциях скоростей двух точек фигуры + пример с решением |
| Мгновенный центр скоростей фигуры |
| Предмет динамики и две ее основные задач |
| Основные законы динамики |

