Задача №21.
Палочка 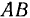 длины а скользит своими концами
длины а скользит своими концами 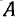 и
и 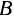 по неподвижным вертикальной и горизонтальной прямым так, что ее конец
по неподвижным вертикальной и горизонтальной прямым так, что ее конец 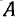 движется с постоянной скоростью
движется с постоянной скоростью 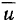 (рис. 64). По палочке движется материальная точка
(рис. 64). По палочке движется материальная точка 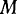 с постоянной относительной скоростью
с постоянной относительной скоростью  . Определить абсолютное ускорение материальной точки
. Определить абсолютное ускорение материальной точки 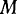 , принимая в качестве параметра, определяющего положение палочки, угол
, принимая в качестве параметра, определяющего положение палочки, угол 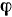 , который она образует с вертикалью.
, который она образует с вертикалью.
Решение:
Для определения ускорения материальной точки воспользуемся теоремой Кориолиса. За относительное движение примем движение материальной точки 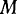 по палочке. Переносное ускорение этой точки можно определить, пользуясь теоремой Ривальса. Примем в качестве полюса точку
по палочке. Переносное ускорение этой точки можно определить, пользуясь теоремой Ривальса. Примем в качестве полюса точку 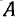 . Тогда ускорение полюса
. Тогда ускорение полюса 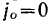 , а ускорение точки
, а ускорение точки 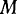 палочки будет зависеть лишь от вращения палочки вокруг точки
палочки будет зависеть лишь от вращения палочки вокруг точки 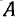 : Заметим, что вертикальная .координата
: Заметим, что вертикальная .координата 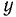 точки
точки 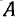 равна:
равна:
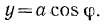
Дифференцируем это выражение и получаем

С другой стороны,
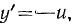
откуда
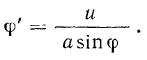
Дифференцируя последнее выражение еще раз, получим
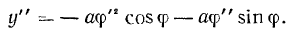
Но так как
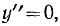
то
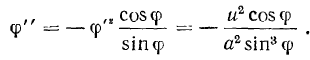
Определим теперь вращательное 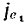 и осестремительное
и осестремительное 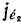 ускорения точки
ускорения точки 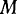 палочки:
палочки:
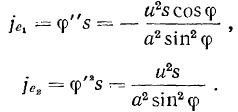
Материальная точка совершает прямолинейное относительное движение с постоянной по величине относительной скоростью 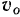 . Поэтому относительное ускорение материальной точки равно пулю. Остается подсчитать добавочное ускорение
. Поэтому относительное ускорение материальной точки равно пулю. Остается подсчитать добавочное ускорение  . Оно будет направлено ортогонально к палочке, в сторону возрастания угла
. Оно будет направлено ортогонально к палочке, в сторону возрастания угла 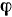 , а по величине равно
, а по величине равно
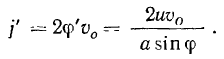
Величину и направление полного ускорения материальной точки можно теперь определить, рассматривая геометрическую сумму составляющих ускорения материальной точки. В результате, как нетрудно видеть, будем иметь
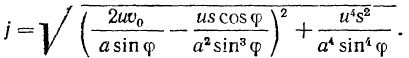
Следует отметить, что удачный выбор подвижной системы отсчета в ряде случаев является залогом успеха в решении задачи.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

