Оглавление:
Принцип Даламбера
В появившемся в 1743 г. сочинении Даламбера «Трактат по динамике» был предложен принцип, сводящий задачу о движении материальной точки к задаче о равновесии и, таким образом, динамику к статике. Принцип этот был призван разрешить или но крайней мере выразить в виде уравнений все задачи механики, причем единым методом.
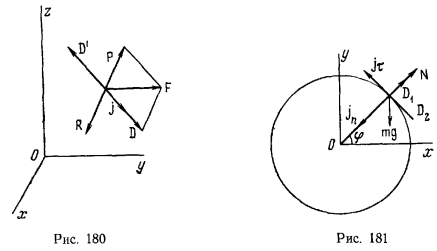
Рассмотрим в неподвижном пространстве материальную точку, на которую наложены некоторые связи и действует активная сила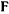 
. Ускорение этой материальной точки в общем случае не будет совпадать с направлением линии действия силы 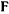. Обозначим через 
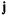ускорение этой точки. Величина и направление ускорения 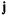определяются некоторой силой 
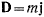, которую нужно приложить к свободной материальной точке, чтобы сообщить ей это ускорение. Силу 
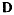называют действующей силой. Тогда активную силу можно представить как сумму двух сил (рис. 180)
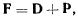
причем часть этой суммы — сила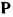 
тратится на преодоление силы реакции связи и называется поэтому потерянной силой. Потерянная сила уравновешивается силой реакции связи
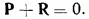
Определяя отсюда силу 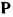, получим для силы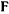
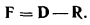
Если к материальной точке приложить теперь силу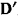 
, равную по величине и противоположную по направлению силе 
:
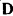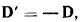
то сила 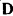будет уравновешиваться силой 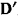. Впоследствии силу 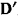стали называть силой инерции. Подставляя в последнее уравнение значение действующей силы 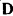, запишем условие равновесия
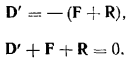
В этом равенстве и заключается принцип Даламбера, который можно сформулировать следующим образом:
Если к активным силам, действующим на материальную точку, добавить силы реакции и силы инерции, то все эти силы будут находиться в равновесии.
По самому определению, сила инерции 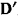равна произведению массы точки на ее ускорение, взятому с обратным знаком
Чтобы найти движение материальной точки из принципа Даламбера, нужно знать реакции связи.
Пример:
Материальная точка вынуждена скользить без трения по гладкой окружности, плоскость которой вертикальна. Определить закон движения точки.
Решение:
На точку действует активная сила — сила тяжести, а положение точки на окружности характеризуется углом 
, который образуется радиусом точки с горизонтальной осью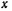 
(рис. 181). Вектор ускорения точки имеет нормальную 
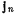и касательную 
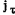составляющие, величины которых можно выразить в функции угла 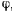и его производных
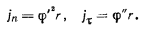
По принципу Даламбера, чтобы уравновесить точку, необходимо приложить к ней кроме активной силы еще силу реакции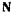 
и силу инерции 
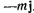. Последняя в рассматриваемом случае имеет две составляющие:
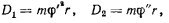
направленные соответственно по радиусу и по касательной к траектории точки в стороны противоположные соответствующим ускорениям. Тогда условие равновесия получит вид
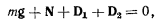
или в проекциях на оси координат
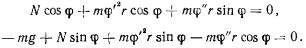
Для определения движения точки из этих уравнений необходимо исключить 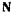, что можно сделать, умножив первое уравнение на 
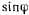, второе — на 
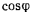и сложив уравнения. Тогда получим
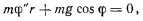
откуда можно найти 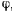как функцию времени. Для определения реакции достаточно теперь подставить в одно из уравнений значения 
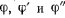, определенные как функции времени.
Петербургскими учеными Я. Германом (1678—1733) и Л. Эйлером (1707—1783) был предложен принцип механики, сводящий задачу о движении материальной точки к задаче о равновесии и получивший название «Петербургский принцип механики», который по существу эквивалентен принципу Даламбера (1716 г.), хотя он был опубликован несколько раньше.
Из принципа Даламбера непосредственно следует, что в каждый момент времени сумма действующей и потерянной сил равна активной силе, действующей на точку
Рассматривая работу сил на произвольном возможном перемещении, получим следующее:
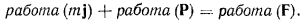
Но потерянные силы уравновешиваются силами реакции
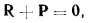
поэтому
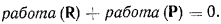
Рассмотрим только идеальные связи, для которых работа сил реакции на любом возможном перемещении точки равна нулю, т. е. работа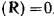 
. Тогда и работа 
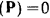, откуда сразу следует
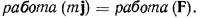
Пусть положение материальной точки определяется декартовыми координатами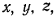 
а возможные перемещения точки 
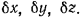Тогда уравнение возможных работ получит вид
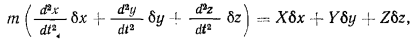
или
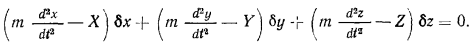
В таком виде принцип был предложен Лагранжем. Само уравнение имеет место для всех действительных движений материальной точки.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Движение несвободной материальной точки |
| Относительное движение материальной точки |
| Кинематика точки |
| Ускорение точки |
