Оглавление:
Относительное движение материальной точки
Вопрос об относительном движении материальной точки тесно связан с основными понятиями механики. Как известно, всякое движение материальной точки можно рассматривать только по отношению к некоторой системе отсчета. Но различные системы отсчета могут совершать движение одна по отношению к другой. Предполагая, что в различных системах отсчета движение материальной точки полостью определяется силами, действующими на эту материальную точку, тотчас приходим к условию, что в различных системах отсчета на точку должны действовать различные силы. Нужно только научиться определять эти силы. В общем случае системы отсчета, относительно которых будет в дальнейшем изучаться движение материальной точки, могут быть неинерциальными системами.
Пусть в некоторой системе отсчета материальная точка с массой 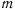 совершает движение под действием силы
совершает движение под действием силы 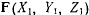 , определенной в этой системе отсчета. В соответствии с законом Ньютона сила
, определенной в этой системе отсчета. В соответствии с законом Ньютона сила 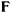 сообщает материальной точке ускорение
сообщает материальной точке ускорение 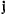 относительно системы отсчета
относительно системы отсчета 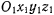 определяемое из условия
определяемое из условия
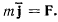
Рассмотрим некоторую другую систему отсчета 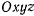 , совершающую некоторое произвольное движение относительно первоначальной системы отсчета
, совершающую некоторое произвольное движение относительно первоначальной системы отсчета 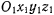 (рис. 173). По теореме Кориолиса ускорение материальной точки относительно системы отсчета
(рис. 173). По теореме Кориолиса ускорение материальной точки относительно системы отсчета 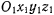 связано с ее ускорением относительно системы отсчета
связано с ее ускорением относительно системы отсчета 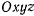 соотношением
соотношением
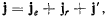
где 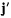 — добавочное ускорение, определяемое но формуле
— добавочное ускорение, определяемое но формуле
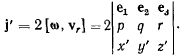
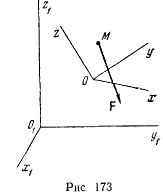
Для сокращения рассуждений в дальнейшем будем первоначальную систему отсчета называть неподвижной системой, а систему отсчета 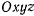 — подвижной системой координат. Вектор
— подвижной системой координат. Вектор 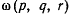 — есть вектор мгновенной угловой скорости вращения подвижном системы координат относительно неподвижной;
— есть вектор мгновенной угловой скорости вращения подвижном системы координат относительно неподвижной; 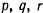 — проекции мгновенной угловой скорости вращения на оси
— проекции мгновенной угловой скорости вращения на оси 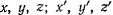 — проекции вектора относительной скорости точки
— проекции вектора относительной скорости точки 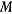 на оси подвижной системы координат. Подставляя значение ускорения в уравнение Ньютона, будем иметь
на оси подвижной системы координат. Подставляя значение ускорения в уравнение Ньютона, будем иметь
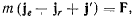
что можно переписать еще в виде
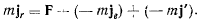
Полученное уравнение движения точки определяет ее ускорение относительно подвижной системы отсчета. Но в правой части этого уравнения появилось два новых члена 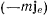 и
и 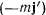 . Эти новые члены имеют значение сил, действующих на материальную точку в подвижной системе координат. Их называют силами К о-р и о л и с а. Будем в дальнейшем называть
. Эти новые члены имеют значение сил, действующих на материальную точку в подвижной системе координат. Их называют силами К о-р и о л и с а. Будем в дальнейшем называть  силой Кориолиса от переносного ускорения, a
силой Кориолиса от переносного ускорения, a 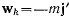 силой Кориолиса от добавочного ускорения. Уравнения движения можно теперь представить в виде
силой Кориолиса от добавочного ускорения. Уравнения движения можно теперь представить в виде
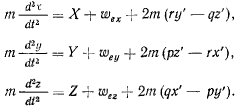
Эти уравнении определяют движение материальной точки относительно подвижной системы координат. Они имеют такой же вид, как и уравнения движения относительно неподвижной системы отсчета. Только в подвижной системе координат движение происходит под действием другой системы сил, действующих на материальную точку. После того как определены силы, действующие на материальную точку в системе 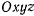 , движение точки относительно этой системы координат можно рассматривать, как и в неподвижной системе координат. Это движение будет происходить в соответствии со вторым законом Ньютона, но под действием новой силы
, движение точки относительно этой системы координат можно рассматривать, как и в неподвижной системе координат. Это движение будет происходить в соответствии со вторым законом Ньютона, но под действием новой силы
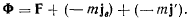
Теорема живых сил в относительном движении точки
Рассмотрим уравнения относительного движения материальной точки, записанные в проекциях на подвижные осн координат 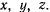 Умножая первое из этих уравнений на
Умножая первое из этих уравнений на 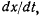 второе на
второе на 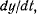 третье на
третье на 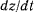 и складывая их, получим
и складывая их, получим
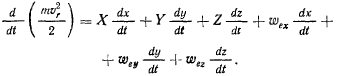
Члены, содержащие добавочное ускорение точки, сюда не войдут, так как
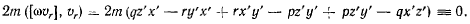
Умножая предыдущее уравнение на 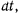 получим
получим
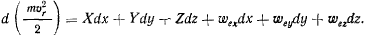
Теорема. Изменение живой силы в относительном движении материальной точки равно работе заданных сил и работе кориоли-совых сил от переносного ускорения на относительном перемещении точки.
Пример:
В неподвижной системе 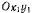 движение материальной точки определяется силой
движение материальной точки определяется силой 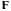 постоянной величины, направленной вдоль неподвижной оси
постоянной величины, направленной вдоль неподвижной оси 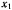 . В начальный момент точка находится на оси
. В начальный момент точка находится на оси 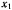 на расстоянии
на расстоянии  от начала координат, а ее скорость
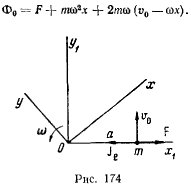
от начала координат, а ее скорость 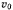 направлена параллельно оси (рис. 174). Определить силу, действующую в начальный момент на материальную точку в системе координат
направлена параллельно оси (рис. 174). Определить силу, действующую в начальный момент на материальную точку в системе координат 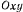 , вращающейся в плоскости
, вращающейся в плоскости 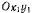 вокруг точки
вокруг точки 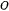 с постоянной угловой скоростью
с постоянной угловой скоростью 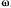 .
.
Решение:
Определим силу 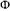 , действующую на точку в системе
, действующую на точку в системе 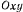 . Переносное ускорение точки
. Переносное ускорение точки
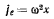
и направлено к точке 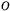 . Для определения добавочного ускорения найдем предварительно относительную скорость точки
. Для определения добавочного ускорения найдем предварительно относительную скорость точки
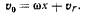
Тогда из матрицы
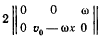
определятся проекции добавочного ускорения
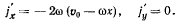
Таким образом, сила 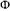 , действующая на точку в начальный момент, направлен по оси
, действующая на точку в начальный момент, направлен по оси  , а ее величина определяется формулой
, а ее величина определяется формулой
Пример:
Материальная точка движется по горизонтальной плоскости, вращающейся с постоянной угловой скоростью 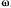 вокруг вертикальной оси. На точку действует сила притяжения к оси вращения
вокруг вертикальной оси. На точку действует сила притяжения к оси вращения
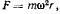
где  — расстояние точки от оси вращения. Исследовать движение точки.
— расстояние точки от оси вращения. Исследовать движение точки.
Решение:
В подвижной системе координат на точку действуют три силы:
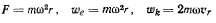
В соответствии с теоремой живых сил существует первый интеграл уравнений движения
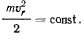
Уравнение движения и проекции на нормаль к траектории дает
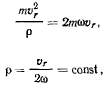
т. е. точка движется по окружности.
Пример:
Исследовать колебания маятника в вагоне, движущемся с постоянным ускорением а по прямолинейным рельсам (рис. 175).
Решение:
На точку 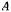 действуют силы
действуют силы
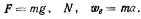
Равнодействующая 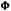 сил
сил 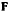 и
и  имеет постоянную величину
имеет постоянную величину 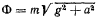 и постоянное направление
и постоянное направление
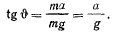
В таком случае период определяется, как и для математического маятника,
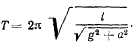
Чем больше величина ускорения а, тем меньше величина периода 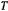 .
.
Уравнения относительного равновесия точки. Чтобы получить уравнения относительного равновесия, нужно в уравнениях относительного движения положить равными нулю относительное ускорение и относительную скорость
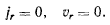
Тогда будет равно нулю и добавочное ускорение, а уравнение относительного равновесия точки запишется в виде
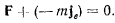
Пример:
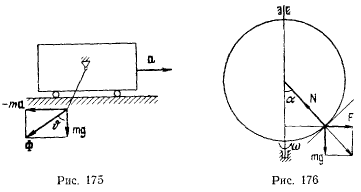
Найти положение относительного равновесия тяжелой материальной точки, вынужденной оставаться на окружности, вращающейся вокруг своего вертикального диаметра с постоянной угловой скоростью 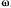 (рис. 176).
(рис. 176).
Решение:
Сила Кориолиса 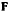 от переносного ускорения направлена от оси вращения и по величине равна
от переносного ускорения направлена от оси вращения и по величине равна 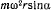 , где
, где  — радиус окружности. Действие на точку силы
— радиус окружности. Действие на точку силы 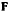 и силы тяжести
и силы тяжести 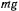 может быть уравновешено только силой реакции
может быть уравновешено только силой реакции 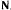 , которая направлена по радиусу окружности к ее центру. Для равновесия необходимо и достаточно, чтобы проекции сил
, которая направлена по радиусу окружности к ее центру. Для равновесия необходимо и достаточно, чтобы проекции сил 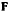 и
и 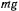 на касательную к окружности были равны и противоположны по знаку, т. е.
на касательную к окружности были равны и противоположны по знаку, т. е.
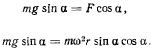
Отсюда получаем три условия равновесия:
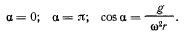
Последнее возможно, если 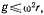 или
или 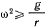 . Силы, действующие на точку в подвижной системе координат, обладают силовой функцией
. Силы, действующие на точку в подвижной системе координат, обладают силовой функцией
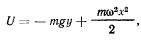
или, выражая 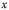 и
и 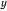 через
через 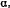
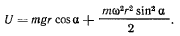
Рассматривая график функции 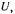 увидим, что при
увидим, что при 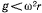 а положениях
а положениях  и
и 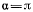 равновесие будет неустойчивым, а в положении, определяемом значением
равновесие будет неустойчивым, а в положении, определяемом значением
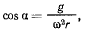
равновесие будет устойчивым. Тот же результат можно получить и из рассмотрения фазовых движений.
- Равновесие материальной точки на поверхности Земли. Вес.
Рассмотрим материальную точку, находящуюся на поверхности Земли. В системе координат, связанной с вращающейся вокруг своей оси Землей, на точку будут действовать: сила притяжения к центру Земли, которую обозначим через 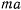 , сила Кориолиса от переносного ускорения
, сила Кориолиса от переносного ускорения 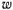 , направленная от оси вращения Земли (рис. 177), и сила реакции (на чертеже не указана). Обозначая через
, направленная от оси вращения Земли (рис. 177), и сила реакции (на чертеже не указана). Обозначая через 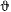 геоцентрическую широту местности, получим силу инерции от переносного ускорения
геоцентрическую широту местности, получим силу инерции от переносного ускорения
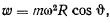
где 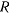 — радиус Земли. Результирующая силы притяжения к центру Земли и силы Кориолиса от переносного ускорения называются весом
— радиус Земли. Результирующая силы притяжения к центру Земли и силы Кориолиса от переносного ускорения называются весом 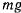 . Угол между линией отвеса и плоскостью экватора называется астрономической широтой местности. Рассматривая проекции сил на оси
. Угол между линией отвеса и плоскостью экватора называется астрономической широтой местности. Рассматривая проекции сил на оси 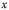 и
и 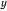 получим
получим
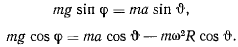
Отсюда найдем зависимость между углами 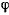 и
и 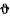 :
:
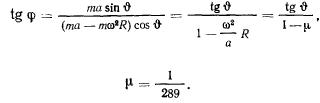
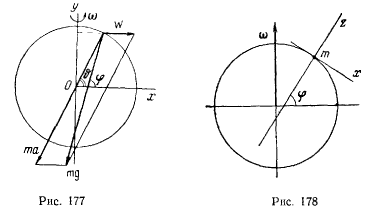
Рассмотрим изменение ускорении силы тяжести с широтой местности:
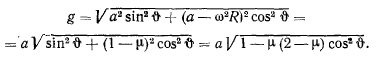
Раскладывая в ряд по формуле бинома
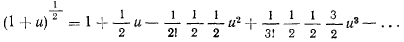
будем иметь приближенное значение для 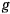 :
:
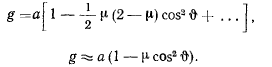
Наименьшее значение 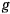 принимает на экваторе, где
принимает на экваторе, где 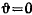
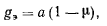
на полюсе же будем иметь
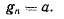
Заметим, что максимальное значение для
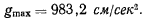
Задача о падении тяжелой точки в пустоте
Рассмотрим вопрос о влиянии вращения Земли на движение свободной материальной точки в пустоте. Движение это будем изучать в местной системе координат. Ось 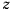 направим вертикально вверх, т. е. по линии действия силы тяжести. Ось
направим вертикально вверх, т. е. по линии действия силы тяжести. Ось  направим перпендикулярно к оси
направим перпендикулярно к оси 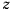 в плоскости меридиана (рис. 178). Кроме силы тяжести на движущуюся точку будет действовать сила Кориолиса от добавочного ускорения. Проекции угловой скорости вращения Земли на подвижные оси координат равны
в плоскости меридиана (рис. 178). Кроме силы тяжести на движущуюся точку будет действовать сила Кориолиса от добавочного ускорения. Проекции угловой скорости вращения Земли на подвижные оси координат равны
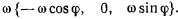
Тогда проекции добавочного ускорения будут
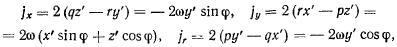
и уравнения движения получат вид
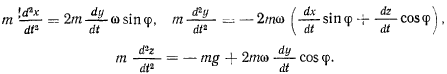
Движение материальной точки определяется системой линейных дифференциальных неоднородных уравнении с постоянными коэффициентами. Нас будет интересовать частное решение этих уравнений, соответствующее начальным условиям
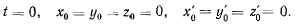
Можно было бы построить общее решение системы дифференциальных уравнений, но это будет связано с громоздкими вычислениями. Поэтому воспользуемся приближенным методом интегрирования уравнений движения — методом последовательных приближений Пикара.
За нулевое приближение возьмем систему 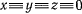 и подставим эти значения координат в правые части уравнений движения. Будем иметь
и подставим эти значения координат в правые части уравнений движения. Будем иметь
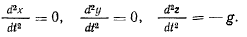
Интегрированием найдем первое приближение
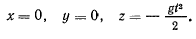
Подставляя эти значения координат в правые части уравнений движения, получим
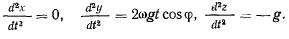
Интегрируя, получим второе приближение
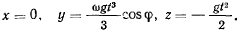
откуда следует, что точка кроме движения по вертикали вниз совершает движение к востоку. Подстановка в правые части исходных дифференциальных уравнений второго приближения дает
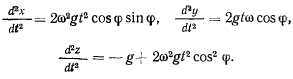
Интегрируя эти уравнения, получаем третье приближение
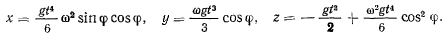
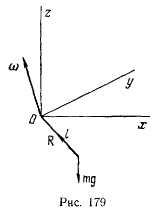
Третье приближение показывает, что точка в своем движении будет отклоняться к югу и к востоку. Эти отклонения легко могут быть объяснены. В самом деле, точка в начальный момент находится в покое относительно вращающейся системы координат. Относительно неподвижной системы координат точка в начальный момент имеет отличную от нуля абсолютную скорость. Заметим, что если время падения равно 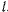 , то отклонение к югу равно 0,04 мм, а отклонение к востоку — 13 см.
, то отклонение к югу равно 0,04 мм, а отклонение к востоку — 13 см.
Маятник Фуко
Маятником Фуко называют сферический маятник длиной 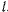 , движение которого рассматривается в системе координат, жестко связанной с вращающейся Землей. Кроме силы Кориолиса от добавочного ускорения на точку действует сила натяжения нити
, движение которого рассматривается в системе координат, жестко связанной с вращающейся Землей. Кроме силы Кориолиса от добавочного ускорения на точку действует сила натяжения нити 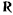 (рис. 179). Уравнения движения принимают вид
(рис. 179). Уравнения движения принимают вид
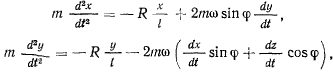
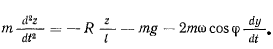
Уравнения движения сферического маятника оказываются более сложными, чем уравнения движения свободной материальной точки, поскольку в эти уравнения входит сила реакции, являющаяся неизвестной функцией координат. Можно пытаться провести интегрирование уравнений методом последовательных приближений, предварительно исключив реакцию. Но и эта задача оказывается весьма сложной. Обычно при исследовании ограничиваются случаем малых колебаний (колебания с малой амплитудой), рассматривая движение приближенным методом. Отношения 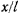 и
и 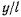 рассматриваются как малые величины, квадратами которых в уравнениях движения можно пренебрегать. В таком случае
рассматриваются как малые величины, квадратами которых в уравнениях движения можно пренебрегать. В таком случае
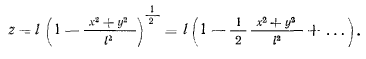
Тогда для малых отклонений

В этом случае из третьего уравнения, отбрасывая бесконечно малые величины, получим
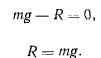
Применим теорему об изменении момента количества движения относительно оси 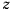 . Для суммы моментов сил относительно оси
. Для суммы моментов сил относительно оси 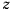 , принимая во внимание, что изменением координаты
, принимая во внимание, что изменением координаты 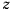 можно пренебречь, получим приближенное значение
можно пренебречь, получим приближенное значение
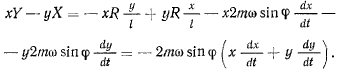
Обозначая через 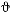 угол, образованный вертикальной плоскостью качания маятника с плоскостью
угол, образованный вертикальной плоскостью качания маятника с плоскостью 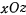 , получим
, получим
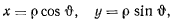
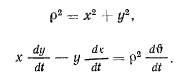
Теорема об изменении момента количества движения дает

Если в начальный момент 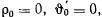 то постоянная интегрирования обращается в нуль, и
то постоянная интегрирования обращается в нуль, и
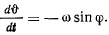
Интегрируя это уравнение, получим
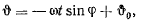
т. е. угол 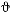 изменяется с течением времени с постоянной скоростью.
изменяется с течением времени с постоянной скоростью.
Обозначая через 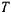 время полного оборота плоскости качания маятника, т. е. время, за которое угол
время полного оборота плоскости качания маятника, т. е. время, за которое угол 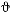 изменится на величину
изменится на величину 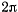 , будем иметь
, будем иметь
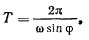
Здесь 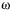 — угловая скорость вращения Земли, так что
— угловая скорость вращения Земли, так что
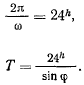
На полюсе при 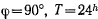 . На экваторе
. На экваторе , и время полного оборота
, и время полного оборота 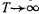 т. е. плоскость качания маятника практически не вращается. Вращение плоскости качания маятника впервые обнаружил в 1851 г. Леон Фуко (1819—1868) в своих знаменитых опытах в Пантеоне. Длина нити была равна 67 л, продолжительность простого колебания 16 сек, широта местности ф равна 48°58′. Время полного оборота плоскости качания, полученное на основании вычислении, оказалось равным 41 час 47 мин, что и было подтверждено опытами. Плоскость качания маятника Фуко, установленного в здании Исаакиевского собора в Ленинграде (длина маятника 98 м, вес 60 кг, амплитуда колебаний 5 м, период колебаний около 20 сек,
т. е. плоскость качания маятника практически не вращается. Вращение плоскости качания маятника впервые обнаружил в 1851 г. Леон Фуко (1819—1868) в своих знаменитых опытах в Пантеоне. Длина нити была равна 67 л, продолжительность простого колебания 16 сек, широта местности ф равна 48°58′. Время полного оборота плоскости качания, полученное на основании вычислении, оказалось равным 41 час 47 мин, что и было подтверждено опытами. Плоскость качания маятника Фуко, установленного в здании Исаакиевского собора в Ленинграде (длина маятника 98 м, вес 60 кг, амплитуда колебаний 5 м, период колебаний около 20 сек, 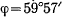 ), поворачивается за каждый час приблизительно на 13°.
), поворачивается за каждый час приблизительно на 13°.
Все приведенные здесь рассуждения носят приближенный характер, так как предполагалось, что длина маятника достаточно велика, а амплитуда колебаний мала. На практике маятник Фуко обычно отпускают из отклоненного начального положения, так что постоянная интегрирования в уравнении
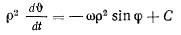
отлична от нуля. Принимая во внимание, что в начальный момент 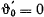 , получим
, получим
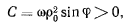
Откуда
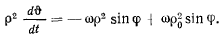
Полагая
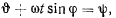
преобразуем последнее уравнение к виду
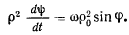
Величины 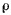 и
и 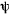 являются относительными полярными координатами горизонтальной проекции точки по отношению к системе осей, вращающейся вокруг вертикали с угловой скоростью
являются относительными полярными координатами горизонтальной проекции точки по отношению к системе осей, вращающейся вокруг вертикали с угловой скоростью 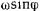 . Для полного исследования движения здесь необходимо принять во внимание еще интеграл живых сил. Тогда уравнения будут совпадать с уравнениями задачи о движении точки, притягиваемой неподвижным центром с силой, пропорциональной расстоянию точки до центра. Известно, что в таком движении точка описывает эллипс.
. Для полного исследования движения здесь необходимо принять во внимание еще интеграл живых сил. Тогда уравнения будут совпадать с уравнениями задачи о движении точки, притягиваемой неподвижным центром с силой, пропорциональной расстоянию точки до центра. Известно, что в таком движении точка описывает эллипс.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Движение точки в сопротивляющейся среде |
| Движение несвободной материальной точки |
| Принцип Даламбера |
| Кинематика точки |

