Оглавление:
Движение несвободной материальной точки
В технических задачах большое значение имеют вопросы движения материальной точки, перемещения которой стесняются связями. Сюда относятся задачи о движении материальной точки по кривой и по поверхности.
Движение материальной точки по кривой.
Наиболее просто представляется движение материальной точки по кривой. Ее положение на кривой определяется всего одним параметром и для полного определения движения точки достаточно определить закон изменения этого параметра со временем.
Рассмотрим движение материальной точки по гладкой материальной кривой 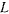 , предполагая, что кривая может со временем менять свою форму и положение относительно системы отсчета
, предполагая, что кривая может со временем менять свою форму и положение относительно системы отсчета 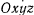 , в которой определены силы, действующие на материальную точку. Кроме активных сил на точку будут действовать еще и силы реакции связи. Так как кривая гладкая, то силы реакции не будут препятствовать перемещению точки по кривой, и полная реакция кривой будет ортогональна к кривой.
, в которой определены силы, действующие на материальную точку. Кроме активных сил на точку будут действовать еще и силы реакции связи. Так как кривая гладкая, то силы реакции не будут препятствовать перемещению точки по кривой, и полная реакция кривой будет ортогональна к кривой.
Будем сначала предполагать, что кривая задана в пространстве, определяемом системой отсчета 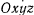 уравнениями
уравнениями
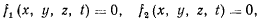
т. е. представляется как геометрическое место точек пересечения двух поверхностей. Пусть 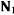 и
и 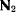 —нормали, проведенные в точке
—нормали, проведенные в точке 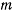 соответственно к поверхностям
соответственно к поверхностям 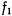 и
и 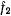 . Вектор
. Вектор 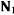 будет коллинеарен с вектором градиента к поверхности
будет коллинеарен с вектором градиента к поверхности 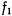 и его проекции будут пропорциональны частным производным
и его проекции будут пропорциональны частным производным
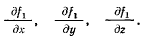
Вектор 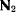 имеет соответственно проекции, пропорциональные частным производным
имеет соответственно проекции, пропорциональные частным производным
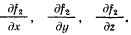
Любая нормаль к кривой 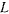 будет лежать в плоскости нормален
будет лежать в плоскости нормален 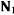 и
и 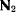 . Обозначая через
. Обозначая через 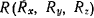 силу реакции кривой
силу реакции кривой 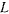 на материальную точку, будем иметь
на материальную точку, будем иметь
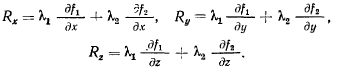
Полагая, что на точку действует еще активная сила 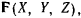 получим уравнения движения точки
получим уравнения движения точки
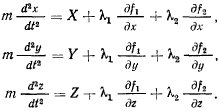
Эти уравнения называются уравнениями Лагранжа первого рода.
а) Теорема живых сил. Умножая уравнения движения соответственно на 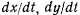 и
и 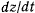 и складывая их, получим в левой части
и складывая их, получим в левой части
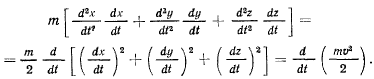
В правой же части будем иметь
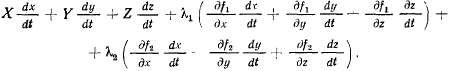
Точка движется в соответствии с наложенными на нее связями, а координаты точки в каждый момент времени удовлетворяют уравнениям поверхностей
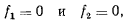
представляющих собой тождества по времени. Дифференцируя эти тождества, будем иметь
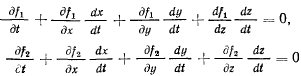
и окончательно получим
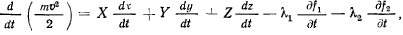
или после умножения на теорему живых сил представим в виде
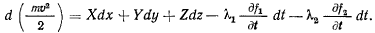
Уравнение получает простой вид, когда связи, наложенные на точку, не зависят явно от времени. Тогда
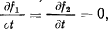
и уравнение запишется следующим образом:
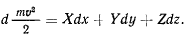
В результате получаем, что если связи, наложенные на материальную точку, не зависят явно от времени, то теорема живых сил получает такой же вид, как и для свободной материальной точки. Если, кроме того, активные силы обладают силовой функцией, зависящей только от координат, т. е. существует функция 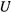 , удовлетворяющая условиям
, удовлетворяющая условиям
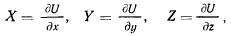
то правая часть уравнения живых сил будет представлять собой полный дифференциал от функции 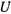 , и уравнение получит вид
, и уравнение получит вид
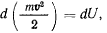
отсюда сразу же получаем первый интеграл уравнений движения— интеграл живых сил
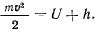
Постоянная живых сил 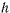 определяется из начальных условий. Мы получаем следующую теорему.
определяется из начальных условий. Мы получаем следующую теорему.
Теорема. Если связи, наложенные на материальную точку, вынужденную оставаться на материальной кривой, не зависят явно от времени, а действующие на точку активные силы обладают силовой функцией, то уравнения движения материальной точки допускают существование первого интеграла — интеграла живых сил.
Качественное исследование движения
Положение материальной точки на кривой может быть определено одним параметром — длиной дуги кривой. Поэтому для решения задачи о движении материальной точки по кривой достаточно всего одного уравнения движения, вместо которого можно принять интеграл живых сил, если только он существует.
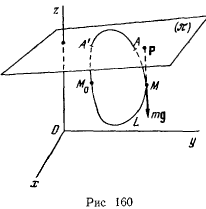
Рассмотрим задачу о движении тяжелой материальной точки 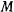 с массой
с массой 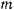 по неподвижной замкнутой кривой с непрерывно меняющейся касательной (рис. 160). В рассматриваемом случае связи, наложенные на материальную точку, не зависят явно от времени, а действующие силы обладают силовой функцией. Поэтому будет существовать интеграл живых сил
по неподвижной замкнутой кривой с непрерывно меняющейся касательной (рис. 160). В рассматриваемом случае связи, наложенные на материальную точку, не зависят явно от времени, а действующие силы обладают силовой функцией. Поэтому будет существовать интеграл живых сил
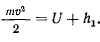
Поскольку ось 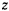 направлена вертикально вверх, получим
направлена вертикально вверх, получим
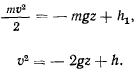
Положив 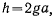 перепишем интеграл в виде
перепишем интеграл в виде
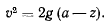
Из этого соотношения видим, что скорость обращается в нуль только на горизонтальной плоскости
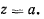
Обозначим эту плоскость через 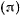 . Если через
. Если через 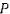 обозначить проекцию точки
обозначить проекцию точки 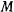 на плоскость
на плоскость 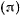 , то для скорости получим значение
, то для скорости получим значение
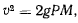
откуда видно, что скорость определяется расстоянием точки 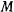 от плоскости
от плоскости 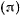 .
.
Может оказаться, что плоскость 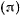 не имеет общих точек с кривой
не имеет общих точек с кривой 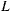 . Если плоскость
. Если плоскость 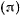 «выше» кривой, то скорость нигде не обращается в нуль, и точка будет двигаться сколь угодно долго по кривой. Ниже кривой плоскость
«выше» кривой, то скорость нигде не обращается в нуль, и точка будет двигаться сколь угодно долго по кривой. Ниже кривой плоскость 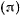 не может быть расположена, так как правая часть равенства
не может быть расположена, так как правая часть равенства 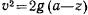 должна быть неотрицательна.
должна быть неотрицательна.
Предположим, что кривая 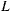 пересекает плоскость
пересекает плоскость 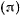 в точках
в точках 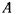 и
и 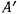 . Обозначая через
. Обозначая через  длину дуги, отсчитываемую от точки
длину дуги, отсчитываемую от точки 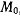 , будем иметь
, будем иметь
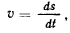
откуда
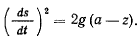
Уравнение кривой позволяет определить
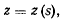
а тогда в предыдущем уравнении можно разделить переменные
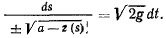
Пусть точка начинает свое движение из положения 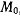 . Обозначим длину дуги
. Обозначим длину дуги 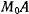 через
через 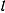 . Обозначая через
. Обозначая через  дугу, определяющую положение точки в некоторый момент времени, и рассматривая
дугу, определяющую положение точки в некоторый момент времени, и рассматривая 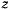 как функцию
как функцию  , разложим
, разложим 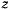 в ряд Тэйлора в окрестности точки
в ряд Тэйлора в окрестности точки 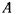
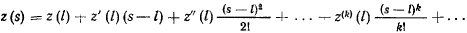
Если производная от 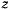 по
по  в точке
в точке 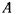 отлична от нуля, то разложение
отлична от нуля, то разложение 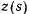 будет начинаться с членов первого порядка малости относительно
будет начинаться с членов первого порядка малости относительно  , а для величины
, а для величины  получим выражение
получим выражение
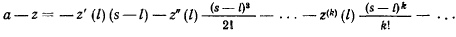
Для точек, лежащих ниже плоскости 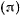 , всегда будем иметь при этом
, всегда будем иметь при этом
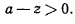
Рассмотрим интеграл
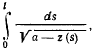
который определяет время движения точки из положения 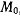 в положение
в положение 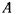 . Этот интеграл является несобственным, так как подынтегральная функция
. Этот интеграл является несобственным, так как подынтегральная функция
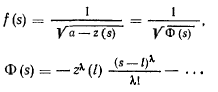
при 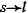 неограниченно возрастает. На основании признака Коши при
неограниченно возрастает. На основании признака Коши при 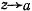 интеграл будет сходиться, если функция
интеграл будет сходиться, если функция 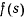 является бесконечно большой порядка
является бесконечно большой порядка 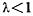 по сравнению с
по сравнению с 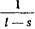 , и будет расходиться, если
, и будет расходиться, если 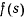 будет порядка
будет порядка 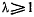 по сравнению с
по сравнению с 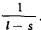 .
.
Если в точке 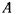 первые
первые 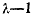 производных от функции
производных от функции 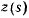 обращаются в нуль, то
обращаются в нуль, то
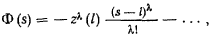
т. е. функция 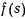 будет иметь порядок
будет иметь порядок 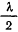 . При
. При 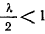 интеграл сходится, а при
интеграл сходится, а при 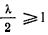 интеграл расходится. В первом случае время, необходимое для достижения точки
интеграл расходится. В первом случае время, необходимое для достижения точки 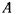 , определяется сходящимся интегралом. После достижения точки
, определяется сходящимся интегралом. После достижения точки 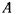 движущаяся материальная точка возвращается к положению
движущаяся материальная точка возвращается к положению 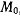 которое она достигает со скоростью
которое она достигает со скоростью 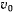 и далее движется к точке
и далее движется к точке 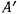 . Движение в этом случае будет иметь колебательный характер. Во втором случае, когда
. Движение в этом случае будет иметь колебательный характер. Во втором случае, когда 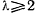
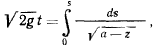
движущаяся точка будет неограниченно приближаться к точке 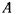 , никогда ее не достигая.
, никогда ее не достигая.
Положение материальной точки на кривой определяется всего одним параметром. Такое движение называют однопараметрическим. Если действующие на точку силы обладают силовой функцией, то движение будет происходить в соответствии с интегралом живых сил. Для изображения состояния движения материальной точки удобно воспользоваться понятием фазовой плоскости, т. е. плоскости, на которой переменные 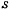 и
и 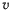 рассматриваются как декартовы координаты точки. Каждая точка фазовой плоскости изображает определенное состояние материальной точки, поэтому такую точку называют изображающей. При движении материальной точки изображающая точка будет описывать некоторую кривую, которая называется фазовой траекторией и не является действительной траекторией движения. Скорость движения изображающей точки называется фазовой скоростью, которая не является скоростью настоящей материальной точки.
рассматриваются как декартовы координаты точки. Каждая точка фазовой плоскости изображает определенное состояние материальной точки, поэтому такую точку называют изображающей. При движении материальной точки изображающая точка будет описывать некоторую кривую, которая называется фазовой траекторией и не является действительной траекторией движения. Скорость движения изображающей точки называется фазовой скоростью, которая не является скоростью настоящей материальной точки.
Если определить силовую функцию как 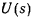 , то интеграл живых сил
, то интеграл живых сил
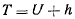
будет определять семейство фазовых траекторий на фазовой плоскости. Задание начального состояния движения материальной точки определяет 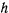 и однозначно определяет фазовую траекторию точки. Семейство фазовых траекторий является одно-параметрическим семейством. Фазовые траектории, соответствующие различным начальным условиям (различным
и однозначно определяет фазовую траекторию точки. Семейство фазовых траекторий является одно-параметрическим семейством. Фазовые траектории, соответствующие различным начальным условиям (различным 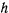 ), между собой не пересекаются, что следует из условия единственности решения уравнений движения. Движение изображающей точки по траектории происходит по часовой стрелке, так как в точках, где
), между собой не пересекаются, что следует из условия единственности решения уравнений движения. Движение изображающей точки по траектории происходит по часовой стрелке, так как в точках, где 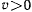 координата
координата 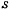 должна возрастать при движении изображающей точки. Состоянию покоя могут соответствовать только точки, находящиеся на оси
должна возрастать при движении изображающей точки. Состоянию покоя могут соответствовать только точки, находящиеся на оси 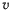 , причем фазовые траектории пересекаются с осью
, причем фазовые траектории пересекаются с осью 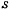 под прямым углом. Точки, в которых обращаются в нуль
под прямым углом. Точки, в которых обращаются в нуль 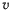 и производная
и производная 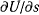 , называются особыми точками фазовой плоскости. В особых точках скорость изображающей точки равна нулю. Все эти точки находятся на оси
, называются особыми точками фазовой плоскости. В особых точках скорость изображающей точки равна нулю. Все эти точки находятся на оси 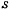 . Зная совокупность фазовых траекторий, можно видеть всю картину возможных движений при различных начальных условиях.
. Зная совокупность фазовых траекторий, можно видеть всю картину возможных движений при различных начальных условиях.
Перепишем интеграл живых сил в виде
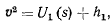
где 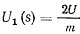 . При помощи этого интеграла легко можно построить фазовые траектории. В самом деле, нетрудно видеть, что все фазовые траектории симметричны относительно оси
. При помощи этого интеграла легко можно построить фазовые траектории. В самом деле, нетрудно видеть, что все фазовые траектории симметричны относительно оси 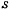 . Геометрическим местом точек, где касательные к фазовым кривым горизонтальны, будут точки, определяемые из уравнения
. Геометрическим местом точек, где касательные к фазовым кривым горизонтальны, будут точки, определяемые из уравнения
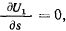
за исключением, быть может, особых точек. Можно предложить следующий способ построения фазовых траекторий. Построим сначала график функции 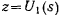 (рис. 161). Пусть некоторые начальные значения определяют постоянную
(рис. 161). Пусть некоторые начальные значения определяют постоянную 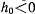 . Построим горизонтальную прямую
. Построим горизонтальную прямую 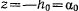 . Разность
. Разность 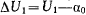 определяет
определяет 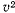 . Если провести другую прямую
. Если провести другую прямую 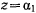 , то получим другую фазовую траекторию. В результате такого построения на фазовой плоскости получим континуум замкнутых кривых, вложенных одна в другую и охватывающих выродившуюся в точку фазовую траекторию. Особая точка здесь соответствует положению равновесия материальной точки.
, то получим другую фазовую траекторию. В результате такого построения на фазовой плоскости получим континуум замкнутых кривых, вложенных одна в другую и охватывающих выродившуюся в точку фазовую траекторию. Особая точка здесь соответствует положению равновесия материальной точки.
Особая точка типа «центр» будет соответствовать устойчивому положению равновесия материальной точки. Особая точка седлового типа соответствует неустойчивому состоянию равновесия. Нетрудно видеть, что в первом случае особая точка соответствует максимуму силовой функции, а в случае седловой точки будем иметь минимум силовой функции. Фазовые траектории с самопересечением называются сепаратрисами.
Математический маятник
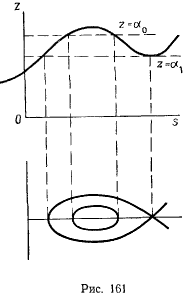
В качестве примера рассмотрим движение материальной точки по окружности радиуса  . Положение точки на окружности определим центральным углом
. Положение точки на окружности определим центральным углом 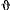 (рис. 162). Тогда
(рис. 162). Тогда
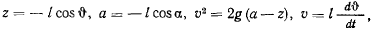
так что
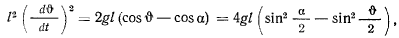
отсюда находим
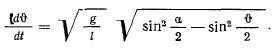
Если наинизшее положение является начальной точкой, тогда, интегрируя, получим
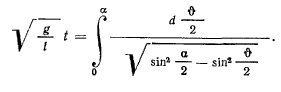
Выполним замену переменной 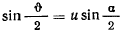 и положим
и положим
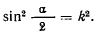
Так как при 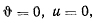 , а при
, а при 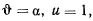 и, кроме того,
и, кроме того,
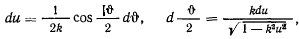
то
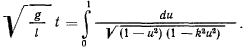
Таким образом, время движения материальной точки (четверть периода) выражается через эллиптический интеграл первого рода. Но выражение
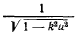
можно разложить в ряд
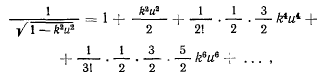
и тогда задача сведется к вычислению интегралов типа
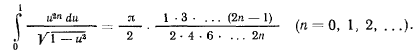
Отсюда для периода получим
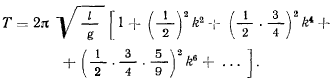
Если амплитуда колебаний 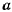 достаточно мала, то в разложении для периода колебаний можно пренебрегать членами, содержащими
достаточно мала, то в разложении для периода колебаний можно пренебрегать членами, содержащими 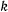 . Приближенное значение периода в этом случае будет
. Приближенное значение периода в этом случае будет
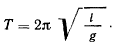
Если период вычисляется по этой формуле, то уже при амплитуде в 20° ошибка периода достигает 0,8%, при 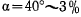 , a при
, a при 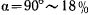 . Для математического маятника, длина которого
. Для математического маятника, длина которого 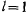 , при амплитуде 90° ошибка периода достигает 1 сек.
, при амплитуде 90° ошибка периода достигает 1 сек.
Циклоидальный маятник
Нидерландский математик и механик Христиан Гюйгенс (1629—1695) изобрел маятник, период колебаний которого не зависит от амплитуды колебаний (изохронный маятник). Оказалось, что период не зависит от амплитуды, если точка движется по циклоиде.
Циклоида представляет собой кривую, которую описывает точка обода круга, катящегося по неподвижной прямой (рис. 163).
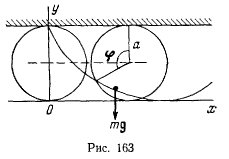
Пусть циклоида имеет горизонтальное основание, расположена в вертикальной плоскости и обращена своей вогнутостью вверх. За ось 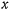 примем неподвижную горизонтальную прямую, касающуюся циклоиды в нижней точке, ось
примем неподвижную горизонтальную прямую, касающуюся циклоиды в нижней точке, ось 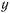 направим вертикально вверх. Уравнение циклоиды можно параметрически представить в виде
направим вертикально вверх. Уравнение циклоиды можно параметрически представить в виде
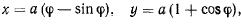
откуда
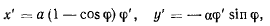
скорость точки
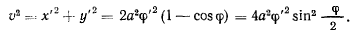
Применяя интеграл живых сил
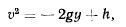
получим
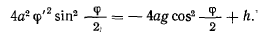
Пусть при 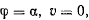 тогда
тогда 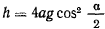 и интеграл живых сил приобретает вид
и интеграл живых сил приобретает вид
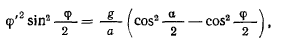
или
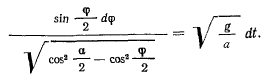
Полагая
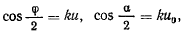
получим
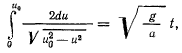
откуда будем иметь
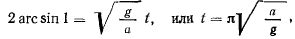
т. е. время движения точки до самого низшего положения не зависит от начального положения точки (от амплитуды).
Определение реакции
Если для изучения движения точки по кривой применить естественные уравнения движения, то будем иметь одно уравнение, определяющее само движение точки, и два уравнения для определения реакции
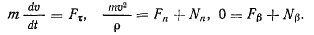
Первое из этих уравнений эквивалентно теореме живых сил и приводит к интегралу живых сил, если выполнены условия существования последнего.
Пример:
Шарик, масса которого равна 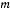 , нанизан на горизонтальную проволочную окружность радиуса
, нанизан на горизонтальную проволочную окружность радиуса  . Зная коэффициент трения
. Зная коэффициент трения 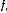 . определить, какую начальную скорость нужно сообщить шарику, чтобы он сделал по окружности один полный оборот.
. определить, какую начальную скорость нужно сообщить шарику, чтобы он сделал по окружности один полный оборот.
Решение:
На точку действуют три силы: сила тяжести, нормальная реакция и сила трения. Составим уравнения движения точки
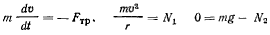
Последние два уравнения дают модуль полной реакции
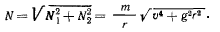
При помощи этого соотношения приведем первое уравнение движения к виду
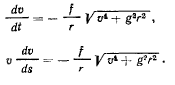
Разделяя переменные, будем иметь

Но
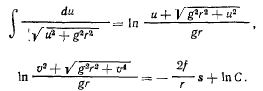
При
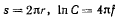
а при
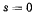
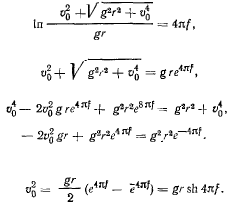
Движение материальной точки по поверхности
Вторым важным для приложений случаем движения несвободной материальной точки является случай движения точки по поверхности.
Предположим, что в своем движении материальная точка все время остается на некоторой гладкой поверхности
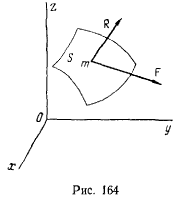
которая стесняет ее перемещения. Форма и положение поверхности могут изменяться со временем, а сама поверхность оказывает воздействие на точку. Это воздействие можно определить некоторой силой, которую называют силой реакции. Она не препятствует перемещению точки по поверхности и направлена по нормали к поверхности (рис. 164), так как по предположению поверхность является гладкой. Аналитически это условие можно представить в виде
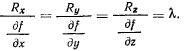
Движение точки полностью определяется двумя силами: активной силой  и силой реакции
и силой реакции 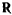 , а уравнения движения имеют вид
, а уравнения движения имеют вид
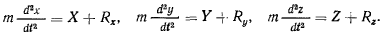
Неизвестные величины 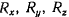 можно заменить одной неизвестной величиной
можно заменить одной неизвестной величиной 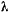 , после чего уравнения перепишутся следующим образом:
, после чего уравнения перепишутся следующим образом:
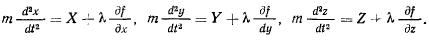
Уравнение 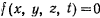 связывает координаты точки и является уравнением связи. Три уравнения движения вместе с уравнением связи полностью определяют движение материальной точки. Сами уравнения называются уравнениями Лагранжа с множителями.
связывает координаты точки и является уравнением связи. Три уравнения движения вместе с уравнением связи полностью определяют движение материальной точки. Сами уравнения называются уравнениями Лагранжа с множителями.
Теорема живых сил
При изучении движения несвободной материальной точки большое значение имеют общие теоремы динамики материальной точки, и в первую очередь теорема живых сил.
Если точка вынуждена оставаться на поверхности
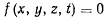
и определен закон движения точки, то ее координаты являются некоторыми функциями времени, после подстановки которых в уравнение связи, последнее становится тождеством. Дифференцируя это тождество по времени, будем иметь
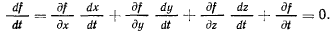
Здесь 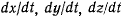 — проекции скорости точки на декартовы оси координат в действительном движении точки.
— проекции скорости точки на декартовы оси координат в действительном движении точки.
Чтобы получить теорему живых сил, умножим каждое из уравнений движения соответственно на 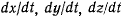 и сложим результат
и сложим результат
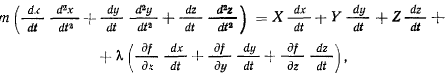
все это преобразуется к виду
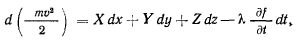
и в результате получаем теорему живых сил для материальной точки, движущейся по поверхности.
Теорема. Изменение живой силы материальной точки равно работе заданных сил на действительном перемещении точки и некоторому дополнительному члену
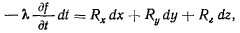
представляющему работу сил реакций связи на действительном перемещении точки.
Если поверхность неподвижна и не изменяет своей формы, то
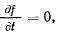
и теорема живых сил приобретает такой же вид, как и для свободной материальной точки, т. е.
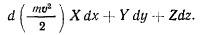
Если, кроме того, активные силы обладают силовой функцией, то будет существовать интеграл живых сил
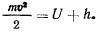
Для существования интеграла живых сил достаточно, чтобы связи не зависели явно от времени и активные силы обладали силовой функцией.
Естественные уравнения движения точки по поверхности
Положение материальной точки на поверхности определяется двумя параметрами. Для нахождения зависимости этих параметров от времени необходимо иметь по крайней мере два дифференциальных уравнения движения. Одной теоремы живых сил теперь уже оказывается недостаточно. Уравнения движения в декартовых координатах часто оказываются очень сложными, поэтому приходится искать другие пути решения задачи о движении.
Предположим, что уравнение поверхности, на которой вынуждена оставаться материальная точка, не содержит явно времени. Точка tn в своем движении по поверхности опишет некоторую траекторию, полностью расположенную на этой поверхности. Рассматривая уравнения движения в проекциях на естественные оси координат (рис. 165), замечаем, что касательная к траектории будет расположена в касательной плоскости к поверхности, а нормальная реакция будет давать проекции только на нормаль и бинормаль
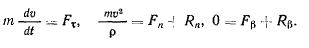
Если активная сила на точку не действует, т. е. 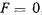 , то из первого уравнения находим
, то из первого уравнения находим
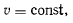
следовательно, точка будет двигаться по поверхности с постоянной скоростью. Из последнего уравнения движения следует, что 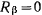 , а потому реакция будет расположена в соприкасающейся плоскости, т. е. нормаль к траектории будет совпадать с нормалью к по-
, а потому реакция будет расположена в соприкасающейся плоскости, т. е. нормаль к траектории будет совпадать с нормалью к по-
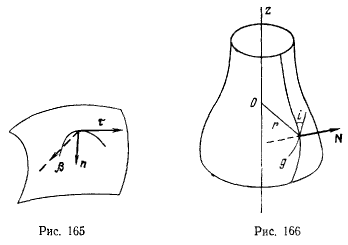
верхности. Кривые, обладающие этим свойством, называются геодезическими. Таким образом, если на точку, движущуюся по поверхности, активные силы не действуют, то точка движется по геодезической кривой с постоянной по величине скоростью.
Движение точки по поверхности вращения. Теорема Клеро
В качестве примера рассмотрим движение материальной точки по поверхности вращения. Пусть ось  — ось симметрии поверхности. Если на точку не действуют активные силы, то точка будет двигаться по геодезической кривой
— ось симметрии поверхности. Если на точку не действуют активные силы, то точка будет двигаться по геодезической кривой  , образующей с меридианом угол
, образующей с меридианом угол  (рис. 166), причем движение происходит с постоянной по величине скоростью. Единственной силой, действующей на точку, будет сила нормальной реакции поверхности
(рис. 166), причем движение происходит с постоянной по величине скоростью. Единственной силой, действующей на точку, будет сила нормальной реакции поверхности 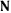 , направленная ортогонально к поверхности. Линия действия этой силы пересекает ось
, направленная ортогонально к поверхности. Линия действия этой силы пересекает ось 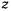 . Из теоремы об изменении момента количества движения точки относительно оси
. Из теоремы об изменении момента количества движения точки относительно оси 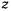 будем иметь
будем иметь
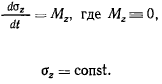
Подставляя сюда явное выражение для момента количества движения, получим
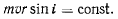
Из постоянства массы и скорости отсюда сразу следует
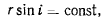
т. е. вдоль геодезической линии поверхности вращения произведение радиуса параллели на синус азимута есть величина постоянная. В этом соотношении заключается теорема Клеро (1713—1765).
Геодезические линии поверхности вращения легко определить, если взять за систему отсчета цилиндрическую систему координат. В этой системе дифференциал дуги
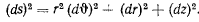
Пусть поверхность задана уравнением
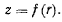
Из интеграла живых сил при отсутствии активных сил получаем
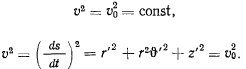
Подставляя сюда 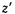 из уравнения поверхности
из уравнения поверхности 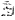
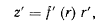
будем иметь
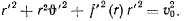
Из интеграла площадей имеем
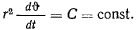
Определяя отсюда 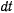 и подставляя в интеграл живых сил, получил
и подставляя в интеграл живых сил, получил
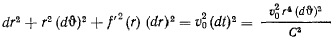
и после разделения переменных приходим к уравнению
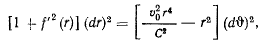
интегрирование которого дает
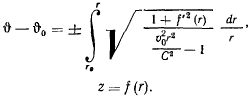
Эти формулы определяют геодезическую кривую на поверхности вращения.
Замечания. 1. Уравнение 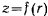 исключает из рассмотрения цилиндрические поверхности вращения
исключает из рассмотрения цилиндрические поверхности вращения 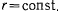 . В последнем случае
. В последнем случае 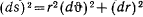 , откуда
, откуда
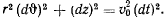
Исключая при помощи интеграла площадей время, найдем
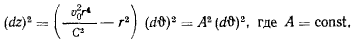
интегрируя найденное уравнение, получим
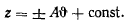
Это и есть уравнение винтовой линии.
- Можно уравнения движения точки отнести к специальным осям
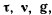 имеющим начало в движущейся точке. Здесь
имеющим начало в движущейся точке. Здесь 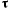 — единичный вектор касательной к траектории точки, направленный в сторону движения;
— единичный вектор касательной к траектории точки, направленный в сторону движения; 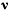 — единичный вектор внутренней нормали к поверхности, а единичный вектор
— единичный вектор внутренней нормали к поверхности, а единичный вектор 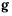 расположен в касательной плоскости перпендикулярно к
расположен в касательной плоскости перпендикулярно к 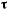 так, чтобы векторы
так, чтобы векторы 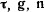 образовывали правую систему (рис. 167). Обозначим через
образовывали правую систему (рис. 167). Обозначим через 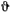 угол между направлением главной нормали траектории
угол между направлением главной нормали траектории 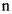 и вектором
и вектором 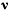 . Проектируя уравнения движения на оси
. Проектируя уравнения движения на оси 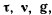 получим
получим
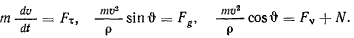
Первое и второе уравнения определяют движение точки по поверхности, последнее же служит для определения реакции поверхности.
В целях дальнейшего преобразования уравнений рассмотрим произведение
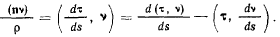
Скалярное произведение 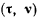 в силу ортогональности векторов равно нулю, так что
в силу ортогональности векторов равно нулю, так что
Для всех траекторий, имеющих одну и ту же касательную в точке, будем иметь
Для траектории, расположенной в плоскости нормального сечения, имеем 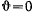 . Если обозначить через
. Если обозначить через 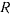 радиус кривизны нормального сечения, то получим
радиус кривизны нормального сечения, то получим
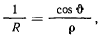
т. е. радиус кривизны произвольной кривой на поверхности вращения по своей абсолютной величине равен проекции на ее соприкасающуюся плоскость радиуса кривизны нормального сечения, имеющего с траекторией общую касательную (теорема Менье). Теперь уравнения движения можно представить в виде
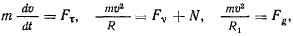
где 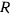 — радиус кривизны нормального сечения, а величина
— радиус кривизны нормального сечения, а величина
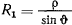
называется радиусом геодезической кривизны (рис. 168).
Сферический маятник
Рассмотрим задачу о движении тяжелой материальной точки по поверхности сферы. Связь эта может быть реализована в виде нерастяжимого и несжимаемого стержня, не имеющего массы, соединяющего точку 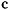 началом координат. На точку действует сила тяжести
началом координат. На точку действует сила тяжести 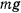 и сила реакции
и сила реакции 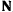 , направленная вдоль стержня. Если реакция всегда направлена к центру, то связь можно осуществить при помощи нерастяжимой идеальной нити. Уравнение связи имеет вид
, направленная вдоль стержня. Если реакция всегда направлена к центру, то связь можно осуществить при помощи нерастяжимой идеальной нити. Уравнение связи имеет вид
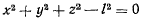
и не содержит явно времени. Ось 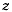 направим вертикально вверх. Активная сила — сила тяжести — допускает существование силовой функции
направим вертикально вверх. Активная сила — сила тяжести — допускает существование силовой функции
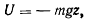
а значит, существует интеграл живых сил
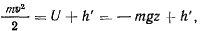
который можно представить в виде
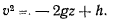
Момент активных сил и сил реакции связи относительно оси 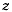 равен нулю, поэтому из теоремы об изменении момента количества движения относительно оси
равен нулю, поэтому из теоремы об изменении момента количества движения относительно оси 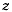 имеем
имеем
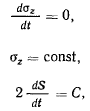
где 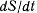 секторная скорость точки.
секторная скорость точки.
Задачу удобнее решать в цилиндрических координатах 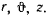 В этих координатах интеграл живых сил и интеграл площадей получают вид
В этих координатах интеграл живых сил и интеграл площадей получают вид
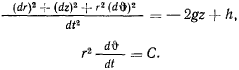
Уравнение связи в цилиндрических координатах получает вид
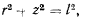
откуда дифференцированием находим
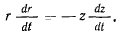
Переписывая теперь интеграл живых сил
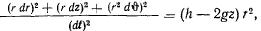
преобразуем его к виду
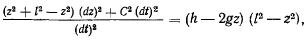
окончательно получим
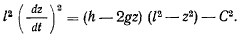
Полученное уравнение позволяет найти закон изменения координаты 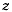 . Перепишем его в виде
. Перепишем его в виде
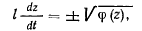
где
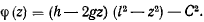
Разделяя переменные и интегрируя, получим
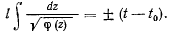
Так как 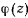 представляет собой многочлен третьей степени относительно
представляет собой многочлен третьей степени относительно 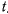 , то стоящий слева интеграл является эллиптическим. После того, как будет найдено tt из последнего соотношения можно определить и уравнение траектории: с этой целью с помощью интеграла площадей исключим из дифференциального уравнения движения время и получим дифференциальное уравнение траектории
, то стоящий слева интеграл является эллиптическим. После того, как будет найдено tt из последнего соотношения можно определить и уравнение траектории: с этой целью с помощью интеграла площадей исключим из дифференциального уравнения движения время и получим дифференциальное уравнение траектории
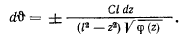
Как видно, задача об определении траектории также сводится к эллиптическим квадратурам.
Качественное исследование движения сферического маятника
Если вектор начальной скорости точки лежит в вертикальной плоскости, то движение будет происходить в той же плоскости. Для этого случая 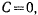 , т. е.
, т. е. 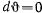 . Следовательно, задача сводится к обыкновенному математическому маятнику, который изучался выше.
. Следовательно, задача сводится к обыкновенному математическому маятнику, который изучался выше.
Если 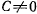 , то, как видно из квадратур,
, то, как видно из квадратур, 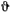 будет монотонной функцией относительно
будет монотонной функцией относительно 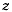 . Для изучения закона изменения функции
. Для изучения закона изменения функции 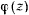 рассмотрим график (рис. 169) функции
рассмотрим график (рис. 169) функции

Нетрудно заметить, что

Для больших по модулю значений 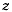
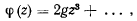
и знак функции определяется знаком первого члена разложения
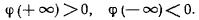
На интервале 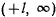 , находится по крайней мере один корень
, находится по крайней мере один корень 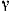 уравнения
уравнения 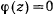 . Координаты, определяемые полученными выше дифферециальными уравнениями, будут принимать вещественные значения только при условии, что подкоренное выражение
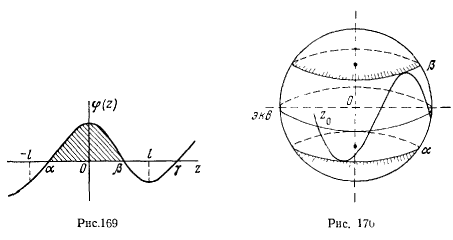
. Координаты, определяемые полученными выше дифферециальными уравнениями, будут принимать вещественные значения только при условии, что подкоренное выражение 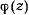 неотрицательно. Пусть сначала начальное значение
неотрицательно. Пусть сначала начальное значение 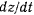 веществен-
веществен-
но и отлично от нуля. Тогда 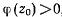 , и имеются действительные корни
, и имеются действительные корни 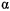 и
и 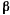 уравнения
уравнения 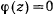 в промежутках
в промежутках 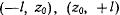 . Действительное движение происходит на интервале, где
. Действительное движение происходит на интервале, где 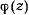 неотрицательно, т. е. между корнями
неотрицательно, т. е. между корнями 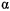 и
и 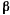 . Представим полином
. Представим полином 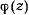 в виде
в виде
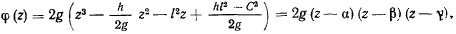
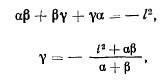
а так как 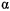 и
и 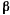 по модулю меньше
по модулю меньше 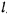 , то, следовательно, числитель положителен. Но
, то, следовательно, числитель положителен. Но 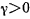 , поэтому
, поэтому
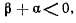
отсюда следует, что по меньшей мере один из корни 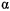 и
и 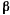 отрицателен, т. е. во всяком случае
отрицателен, т. е. во всяком случае
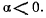
Корень 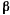 может быть как положительным, так и отрицательным (рис. 170). Пусть для определенности при
может быть как положительным, так и отрицательным (рис. 170). Пусть для определенности при 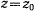 координата
координата  убывает. Тогда перед корнем надлежит взять знак минус, и
убывает. Тогда перед корнем надлежит взять знак минус, и  будет уменьшаться до тех пор, пока не достигнет значения
будет уменьшаться до тех пор, пока не достигнет значения 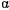 . Из интеграла площадей следует, что угол
. Из интеграла площадей следует, что угол 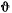 изменяется лишь в одну сторону,
изменяется лишь в одну сторону, 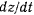 может изменить знак лишь когда
может изменить знак лишь когда 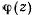 обращается в нуль, т. е. при
обращается в нуль, т. е. при  или
или 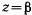 . Если в начальный момент
. Если в начальный момент 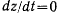 то
то 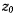 является корнем уравнения
является корнем уравнения 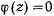 мы имеем критический случай. Дифференциальное уравнение для
мы имеем критический случай. Дифференциальное уравнение для 
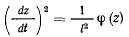
можно преобразовать к виду
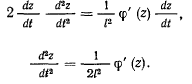
Если  и
и  простые корни, то всюду
простые корни, то всюду 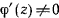 , и тогда будет происходить изменение координаты
, и тогда будет происходить изменение координаты  . Если
. Если 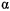 и
и 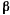 — кратные корни, то
— кратные корни, то 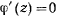 . В этом случае точка описывает окружность в плоскости, перпендикулярной к оси
. В этом случае точка описывает окружность в плоскости, перпендикулярной к оси  .
.
Определение реакции
Реакция не входит в выражение для первых интегралов, и для ее определения следует исходить не из первых интегралов, а из самих уравнений движения материальной точки. Пусть 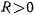 тогда, когда реакция направлена к центру. Тогда уравнения движения в проекциях на декартовы оси координат запишутся в виде
тогда, когда реакция направлена к центру. Тогда уравнения движения в проекциях на декартовы оси координат запишутся в виде
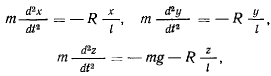
а интеграл живых сил
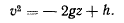
Умножая уравнения движения соответственно на  и складывая, получим
и складывая, получим
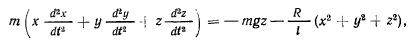
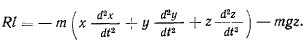
Дифференцируя по времени уравнение связи
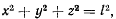
будем иметь
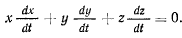
Повторное дифференцирование дает
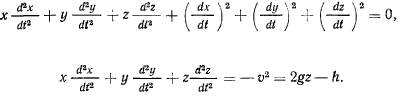
В результате приходим к следующему уравнению для определения реакции:
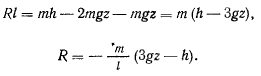
Отсюда видно, что в задаче о движении сферического маятника реакция кроме постоянной 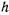 зависит только от координаты
зависит только от координаты  . Следовательно, на одинаковых параллелях реакции будут численно равны. Если при определении реакции получим во все время движения
. Следовательно, на одинаковых параллелях реакции будут численно равны. Если при определении реакции получим во все время движения 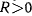 что всегда выполняется при
что всегда выполняется при
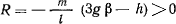
то маятник можно осуществить при помощи гибкой нерастяжимой нити. Если же во время движения 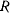 обращается в нуль, то связь перестает быть натянутой, и после освобождения точки от связи приходим к новой механической задаче — задаче о движении свободной материальной точки.
обращается в нуль, то связь перестает быть натянутой, и после освобождения точки от связи приходим к новой механической задаче — задаче о движении свободной материальной точки.
Малые колебания сферического маятника
Запишем уравнения связи для сферического маятника в виде
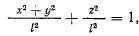
откуда для отношения 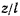 получим значение
получим значение
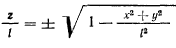
и будем рассматривать малые отклонения маятника от вертикали, проходящей через начало координат. Тогда величина
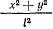
будет оставаться малой по сравнению с единицей, и приближенно можно считать, что
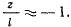
Верхнее положение точки является положением равновесия, но это положение неустойчиво, поскольку нижняя параллель всегда ниже экватора. Третье уравнение движения дает
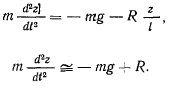
При этом в положении равновесия
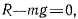
откуда
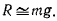
Если это условие не выполняется, то в силу того, что
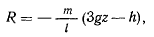
a 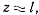 будем иметь
будем иметь 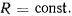 Тогда из уравнения движения имеем
Тогда из уравнения движения имеем
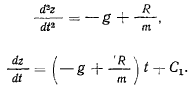
Но производная здесь не может неограниченно возрастать со временем, если 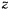 остается ограниченной величиной. Координаты
остается ограниченной величиной. Координаты 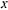 и
и 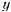 точки
точки 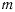 определяются приближенными уравнениями
определяются приближенными уравнениями
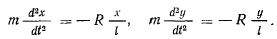
Принимая во внимание, что 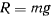 , представим эти уравнения в виде
, представим эти уравнения в виде
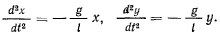
Положив 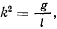 получим общее решение системы уравнения движения
получим общее решение системы уравнения движения
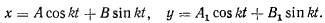
Не нарушая общности, положим, что при точка находится на оси 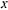 , а начальная скорость направлена перпендикулярно к этой оси. Тогда будем иметь
, а начальная скорость направлена перпендикулярно к этой оси. Тогда будем иметь
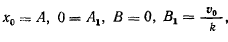
и соответствующее частное решение запишется в виде
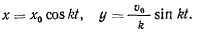
Исключая время, получим уравнение,
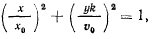
которое представляет собой уравнение траектории проекции точки на плоскость  , т. е. движение проекции точки происходит по эллиптической траектории.
, т. е. движение проекции точки происходит по эллиптической траектории.
Пример:
Тяжелая материальная точка движется по внутренней поверхности прямого кругового конуса, вершина которого обращена вниз, ось симметрии вертикальна, угол при вершине равен 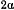 . В начальный момент расстояние точки от вершины конуса равно
. В начальный момент расстояние точки от вершины конуса равно  , начальная скорость равна
, начальная скорость равна 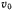 и направлена перпендикулярно к образующей конуса. Определить траекторию точки и давление, оказываемое ею на поверхность конуса.
и направлена перпендикулярно к образующей конуса. Определить траекторию точки и давление, оказываемое ею на поверхность конуса.
Решение:
Положение точки на поверхности конуса можно задать двумя координатами. В качестве таких координат выберем расстояние точки от вершины конуса  и угол
и угол 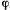 , который образует вертикальная плоскость
, который образует вертикальная плоскость 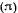 , проходящая через ось симметрии конуса и точку
, проходящая через ось симметрии конуса и точку 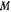 , с неподвижной плоскостью
, с неподвижной плоскостью 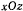 . Рассматривая движение точки как сложное, состоящее из прямолинейного относительного движения в плоскости
. Рассматривая движение точки как сложное, состоящее из прямолинейного относительного движения в плоскости 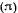 и переносного вращения вместе с плоскостью
и переносного вращения вместе с плоскостью 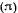 вокруг оси
вокруг оси  , будем иметь
, будем иметь
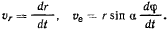
Ha точку действуют только сила тяжести и нормальная реакция гладкой поверхности, поэтому существует интеграл живых сил
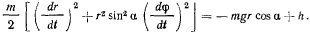
Кроме того, действующие силы не создают момента относительно оси  , поэтому существует интеграл площадей
, поэтому существует интеграл площадей
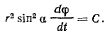
Постоянные  и
и 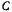 выражаются через начальные данные
выражаются через начальные данные
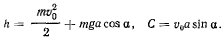
Дна первых интеграла позволяют определить траекторию точки на поверхности конуса. В самом деле, исключая время, получим
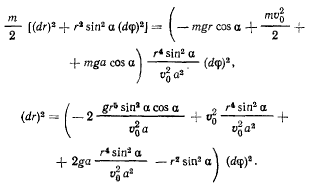
Откуда уравнение траектории получается в квадратурах
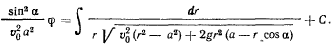
Для определения давления точки на поверхность конуса можно было бы воспользоваться естественными уравнениями движения, но такой путь оказывается сложным, поскольку он требует знания траектории точки. Поэтому рассмотрим векторное уравнение движения точки
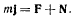
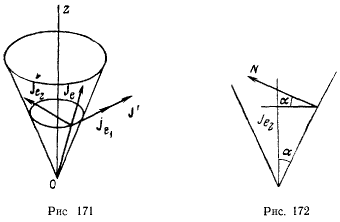
Давление точки на поверхность равно по величине и противоположно по направлению силе реакции 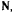 , которая зависит от активных сил, действующих на точку, и ускорения, с которым движется точка. Для определения давления требуется знать проекцию ускорения точки на нормаль к поверхности конуса. Определяя ускорение при помощи теоремы Кориолпса, заметим, что относительное ускорение направлено по образующей конуса, а в переносном движении точка движется по окружности, плоскость которой ортогональна к оси
, которая зависит от активных сил, действующих на точку, и ускорения, с которым движется точка. Для определения давления требуется знать проекцию ускорения точки на нормаль к поверхности конуса. Определяя ускорение при помощи теоремы Кориолпса, заметим, что относительное ускорение направлено по образующей конуса, а в переносном движении точка движется по окружности, плоскость которой ортогональна к оси  и имеет касательную
и имеет касательную 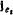 и нормальную
и нормальную 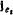 составляющие ускорения (рис 171). Нормальная составляющая ускорения
составляющие ускорения (рис 171). Нормальная составляющая ускорения 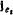 направлена ортогонально к оси симметрии конуса, а по величине равна
направлена ортогонально к оси симметрии конуса, а по величине равна
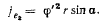
Добавочное ускорение 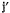 коллинеарно с направлением ускорения
коллинеарно с направлением ускорения 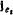 и численно равно
и численно равно
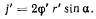
На нормаль к поверхности дает проекцию только составляющая ускорения 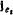 (рис. 172). Проектируя уравнение движения на нормаль к поверхности конуса, получим
(рис. 172). Проектируя уравнение движения на нормаль к поверхности конуса, получим
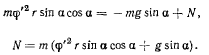
Определив 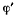 из интеграла площадей
из интеграла площадей
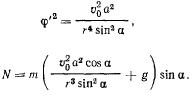
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Движение материальной точки под действием центральных сил |
| Движение точки в сопротивляющейся среде |
| Относительное движение материальной точки |
| Принцип Даламбера |

