Метод неопределенных множителей Лагранжа

Метод неопределенных множителей Лагранжа

Рассмотрим голономную механическую систему, подверженную действию активных сил 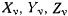и стесненную идеальными связями, аналитические выражения которых имеют вид

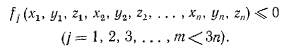
Будем предполагать, что в рассматриваемом положении равновесия все связи оказываются в натянутом состоянии. Кроме того, будем предполагать, что матрица Якоби, составленная из частных производных

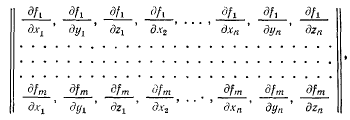
имеет хотя бы один отличный от нуля минор m-того порядка. Тогда при натянутых связях m координат точек системы могут быть представлены в функции 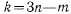остальных.

Сообщив системе произвольное возможное перемещение, заметим, что на этом возможном перемещении либо все связи остаются в натянутом состоянии, либо некоторые из связей освобождаются (переходят в ненатянутое состояние). В самом общем случае возможные перемещения будут подчинены условиям

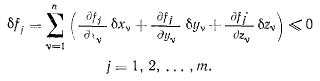
Условие равновесия системы

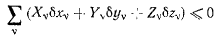
содержит вариации координат 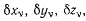которые не могут быть выбраны произвольно, а подчинены условиям (b). Чтобы отсюда получить условия равновесия, следует исключить зависимые вариации координат. Это исключение можно провести, воспользовавшись методом неопределенных множителей Лагранжа. Для этого умножим сначала каждое из условий связи (Ь) на неопределенные пока множители 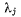и добавим получающийся результат к левой части неравенства (с). В результате получим сумму

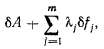
которая обращается в нуль на неосообождающих перемещениях системы. Группируя коэффициенты при одинаковых значениях 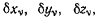для неосвобождающих перемещений будем иметь

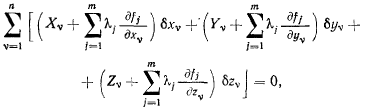
где величины 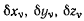подчинены условиям (b) со знаком равенства. Предполагая уравнении связи (b) независимыми, заметим, что m величин 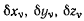являются в этом случае зависящими от 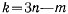остальных. Последние могут принимать произвольные значения. Подберем теперь произвольные множители 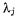таким образом, чтобы коэффициенты при всех, зависимых перемещениях обратились в нуль. Тогда равенство (d) будет выполняться на любом неосвобождающем перемещении системы лишь в том случае, когда все коэффициенты при оставшихся независимых перемещениях 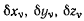обращаются в нуль. Иначе говоря, коэффициенты при m независимых вариациях обращаются в нуль вследствие соответствующего выбора множителей 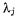а коэффициенты при независимых возможных перемещениях обращаются в нуль потому, что иначе уравнение (d) не будет выполняться на всех возможных перемещениях системы. Таким образом, для удовлетворения уравнения (d) необходимо приравнять нулю асе коэффициенты при 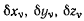в результате чего получим уравнения

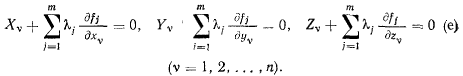
эти 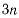уравнений вместе с m уравнениями связи (а) определяют 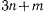неизвестных величин 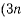координат 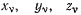в положении равновесия системы и m множителей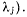

Рассматривая теперь освобождающие перемещения, для которых условия (b) и (с) выполняются со знаком неравенства, нетрудно видеть, что в положении равновесия и для этих перемещений имеет место равенство

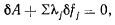
так как в положении равновесия равны нулю все коэффициенты при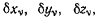

Перепишем равенство (f) в виде

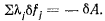
Здесь правая часть равна нулю дли всех неосвобождаюших перемещений системы и больше нуля для освобождающих перемещений, поэтому

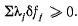
Рассмотрим такое освобождающее перемещение, при котором освобождается только одна связь (например, связь 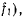так что на этом перемещении будем иметь

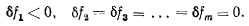
Тогда из условия (g) получим

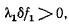
Что возможно лишь при

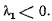
Проводя аналогичные рассуждения для связей 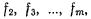придем к заключению, что в положении равновесия все множители к; должны быть отрицательными.

Уравнении (е) называются уравнениями равновесия с множителями Лагранжа. Они справедливы как для освобождающих, так и для неосвобождаюших связей. Положительные значения множителей 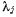не отвечают положениям равновесия системы лишь в том случае, когда рассматриваются освобождающие связи.

Все рассуждения относительно знаков теряют смысл для тех 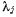которые соответствуют двухсторонним связям. Для этих связей на всех возможных перемещениях системы имеет место условие 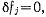поэтому соответствующие множители могут иметь произвольные знаки.

Пример:

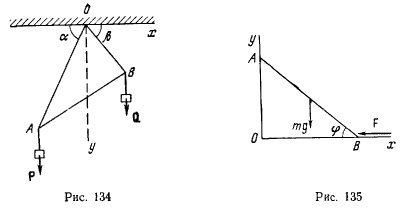
Черед бесконечно малый блок О (рис. 134) перекинута веревка, к концам которой прикреплена невесомая палочка АВ. Найти положение равновесия системы, если на концах палочки подвешены два груза Р и Q.

Решение:

Обозначая через 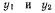вертикальные координаты точек А и В, запишем обшее уравнение статики в виде

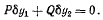
На систему наложены следующие связи:

Условие неизменяемости длины палочки, которое можно представить уравнением

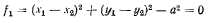
. Условие неизменяемости длины нити (предполагается, что нить все-время находится в натянутом состоянии), которое записывается равенством

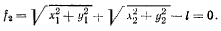
Дифференцируя эти уравнения связи, получим

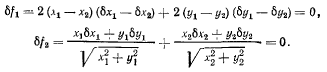
Применяя метод множителей Лагранжа, запишем следующие уравнения равновесия:

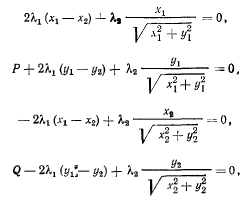
к которым еще необходимо присоединить два уравнения связи. Складывая, уравнения (а) и (с), находим

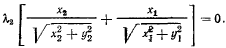
Отсюда следует, что при равновесии один из сомножителей обращается в нуль. Но если бы 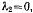то, складывая (b) и (d), мы получили бы

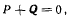
что противоречит условиям задачи. Следовательно, в нуль должен обратиться второй множитель, откуда имеем

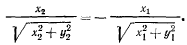
Но из чертежа видно, что

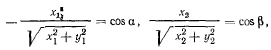
следовательно, 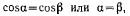т. е. в положении равновесия ветви нити образуют равные углы с осью х.

Умножая теперь первое уравнение на 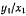и вычитая результат из (b), будем иметь

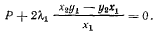
Аналогично из (с) и (d) получим

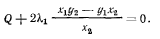
Тогда

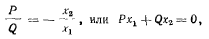
т. е. при равновесии сумма моментов сил Р и Q относительно точки О должна быть равна нулю.

Можно отмстить еще и частные решения полученных уравнении, которые получаются при |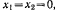 т. е. когда палочка занимает вертикальное положение.

Пример:

Тяжелая однородная палочка АВ скользит своими концами по вертикальной и горизонтальной гладким прямым. К нижнему концу палочки приложена горизонтальная сила F (рис. 135). Определить положение равновесия палочки.

Решение:

Если связи в точках А и В рассматривать как двусторонние, то уравнения связей представятся равенствами

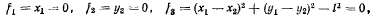
я из принципа Бериулли будем иметь

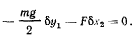
Применяя метод множителей Лагранжа, отсюда получим

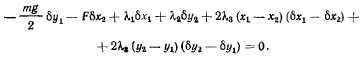
Откуда, приравнивая нулю коэффициенты при 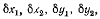будем иметь

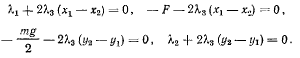
Принимая из условий связи, что 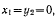эти уравнения можно переписать в виде

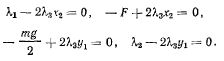
Складывая первое и второе уравнения, получим

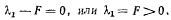
и из третьего и четвертого уравнений найдем

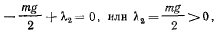
откуда видно, что оба множителя и 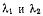положительны.

Умножая второе уравнение на 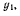третье на 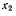и вычитая третье из второго, получим

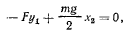
откуда

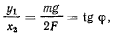
угол 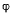определяет положение равновесия системы.

Если наложенные связи являются освобождающими, то уравнении связей запишутся в виде

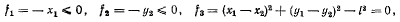
а условие равновесия

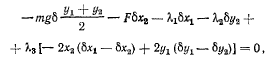
отсюда получим уравнения равновесия

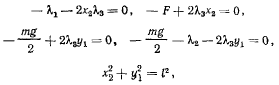
откуда будем иметь

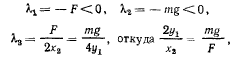
т. е. при равновесии

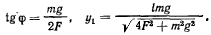
Чтобы получить отрицательное значение для 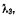необходимо и третью связь рассматривать как освобождающую, предполагая, что расстояние между точками не может быть меньше длины стержня, т. е.

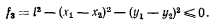
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Обобщенные координаты

Общие теоремы о равновесии системы материальных точек

Определение реакций связи

Определение реакции связи в общем случае