Связи и возможные перемещения
Рассмотрим систему материальных точек положение которых определяется их декартовыми координатами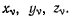 
Если на точки системы не наложено никаких связей, то их координаты 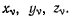могут принимать произвольные значения. Может оказаться, что координаты точек системы подчинены некоторым ограничениям, которые называются связями. Эти связи могут быть представлены в виде равенств или неравенств, ограничивающих область допустимых значений координат точек системы. Если связи представляются в виде равенств
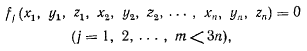
то число их не должно превосходить величины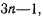 
где n число точек системы. В противном случае при 
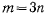уравнения связей будут однозначно определять координаты всех точек системы, и система не сможет перемешаться из положения, определенного связями. Так, например, для точки, вынужденной оставаться на окружности, уравнения связи могут быть представлены в виде
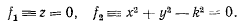
Если связи представляются в виде равенств, то координаты точек системы всегда должны удовлетворять этим равенствам. Такие связи называются удерживающими, или двусторонними.
Связи записываются в виде неравенств (соединенных с равенствами) вида
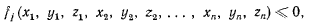
когда точки системы в рассматриваемом положении подчинены условиям, определяемым равенствами, а возможные перемещения таковы, что точки системы могут освобождаться от связей. Такие связи могут ограничивать возможные перемещения системы. Так, например, координаты материальной точки, находящейся внутри материальной сферы, будут подчинены условию
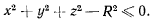
Если связь, накладываемая на некоторую точку системы, осуществляется в виде строгого неравенства, то она будет осуществляться в виде неравенства и в некоторой достаточно малой окрестности этого положения, поэтому она не будет оказывать никаких ограничений на перемещения рассматриваемой точки. Такая связь оказывается несущественной в рассматриваемом положении и при анализе данного положения равновесия может быть отброшена из рассмотрения. Все проведенные рассуждения могут быть распространены и на более общий случай.
Связи, которые записываются в виде неравенств (соединенных с равенствами) в дальнейшем будем называть неудерживающими, или освобождающими связями (односторонними).
Пусть на систему материальных точек наложены удерживающие связи
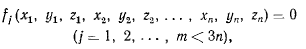
где n число точек системы. Будем предполагать, что матрица Якоби, составленная из частных производных от функций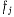 
по всем переменным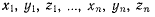 
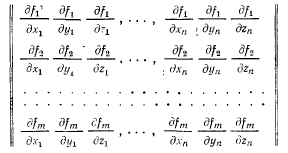
имеет ранг m, т. с. хотя бы один из миноров т-го порядка этой матрицы отличен от нуля. При выполнении этих условий ссе функции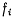 
будут независимыми и ни одна из них не является функцией остальных. Наряду с данным рассмотрим соседнее, бесконечно близкое положение системы, допускаемое наложенными связями. Тогда координаты точек этого нового положения
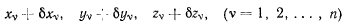
будут также удовлетворять уравнениям связи (а), так что
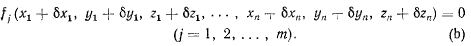
Предполагая, что уравнения связей представлены непрерывными, сколь угодно раз дифференцируемыми функциями, перепишем уравнения (b) в виде степенного ряда но малым значениям величин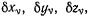 
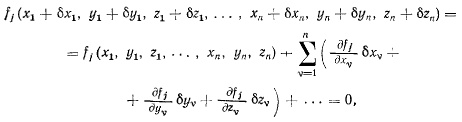
где
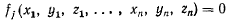
для всех значений координат точек системы.
Для достаточно малых значений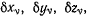 
при которых можно пренебречь членами выше первого порядка малости, получим
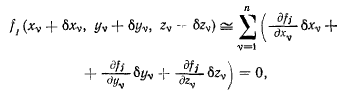
или
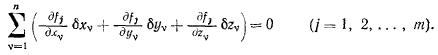
Вариации координат 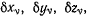удовлетворяют полученным т уравнениям связи и не могут быть все заданы произвольно. Из условия, что матрица, составленная из коэффициентов при 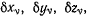имеет ранг m, следует, что m из величин 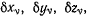являются зависимыми и могут быть выражены через остальные 
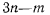независимых величин 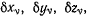Число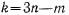 
называют числом степеней свободы системы. Оно равно числу независимых параметров, определяющих положение механической системы. Такими параметрами могут быть как 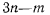независимых декартовых координат, так и криволинейные координаты, в ряде случаев более отвечающие рассматриваемой задаче. Так, например, положение точки на окружности можно задать всего одним параметром, в качестве которого можно выбрать угол, который радиус, соединяющий точку с центром окружности, образует с некоторой заданной прямой.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Принцип возможных перемещения |
| Принцип Торричелли |
| Обобщенные координаты |
| Общие теоремы о равновесии системы материальных точек |
