Оглавление:
Произвольная система сил, действующих на твердое тело
Эквивалентные системы сил
Из основных аксиом статики непосредственно следуют элементарные операции, не изменяющие действия рассматриваемой системы сил на твердое тело:
- Силу можно переносить вдоль ее линии действия.
- Силы, линии действия которых пересекаются в одной точке, можно складывать по правилу параллелограмма (по правилу сложения векторов).
- К системе сил, действующих на твердое тело, можно всегда добавить две силы, равные по величине, лежащие ня одной прямой и направленные Рис. 9G в противоположные стороны.
Эти элементарные операции позволяют установить эквивалентные системы тел, как системы, производящие одинаковое действие на твердое тело.
Пара сил
Система, состоящая из двух параллельных сил, равных по величине, не лежащих на одной прямой и направленных в противоположные стороны, называется парой сил. Пара сил обладает всеми свойствами пары скользящих векторов. Момент m пары сил является свободным вектором, координаты которого определяются при помощи векторного произведения (рис. 96)
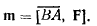
Приведение системы сил, действующих на твердое тело, к произвольной точке (центру приведения)
Систему сил, действующих на твердое тело, можно заменить эквивалентной системой сил, получающейся из данной при помощи элементарных операций. Эта новая система оказывает такое же действие на твердое тело, как и первоначальная система сил. В прикладных задачах представляет интерес замена действующей системы сил более простой эквивалентной системой. Такой более простой системой является система, состоящая из трех сил, одна из которых проходит через произвольную, наперед заданную точку, а две другие представляют собой пару сил. Построение такой системы сил называется приведением системы сил, действующих на твердое тело, к точке. При приведении используются элементарные операции, как это было показано в теории скользящих векторов, путем добавления в наперед заданной точке О нулевой системы сил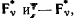 
величины которых равны величине силы 
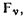действующей на 
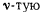точку твердого тела. В результате получается система сил 
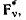линии действия которых проходят через точку О и систему пар с моментами 
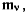определяемыми из условия
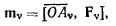
где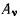 
— точка приложения силы 
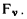Новая система сил эквивалентна одной результирующей силе F, величина и направление которой определяются из условия
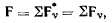
а линия действия проходит через точку О, и паре сил с моментом
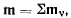
которая называется результирующей парой системы.
В силу обратимости элементарных операций легко показать, что две системы сил будут эквивалентны тогда ц только тогда, когда обе эти системы приводятся к одним и тем же результирующей силе и результирующей паре сил, т. с. когда выполняются условия
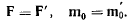
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Различные задачи статики |
| Момент силы |
| Условия равновесия системы сил, действующих на твердое тело |
| Приведение системы сил, действующих на твердое тело, к динаме. Уравнения равновесия твердого тела |
