Мгновенно-винтовое движение твердого тела
Теорема. Сложное мгновенное движение твердого тела, состоящее из одного мгновенно-поступательного движения со скоростью v и одного мгновенно-вращательного движения с угловой скоростью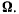 
эквивалентно одному мгновенно-винтовому движению. Доказательство. Рассмотрим мгновенное движение твердого тела, состоящее из мгновенного вращения с угловой скоростью 
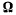линия действия которого проходит через точку О, и мгновенно- поступательного движения со скоростью v (рис. 47). Представим вектор v в виде суммы двух свободных векторов Как было показано выше, система мгновенно-поступательных 
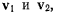один из
которых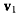 
параллелен вектору 
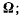а второй 
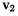ортогонален вектору 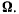В плоскости 
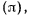проходящей через линию действия вектора 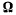и ортогональной к вектору 
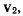выберем такую точку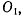 
относительно которой момент вектора 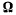по величине совпадает с величиной вектора 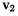а по направлению противоположен направлению вектора 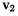Положение точки 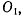определяется из условия
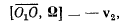
или
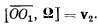
Умножив векторно это равенство на 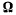получим
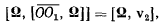
или
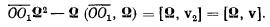
Если, «роме того, потребовать, чтобы отрезок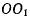 
был ортогонален к линии действия вектора 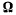то равенство можно будет переписать в виде
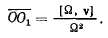
К рассматриваемой системе мгновенных движений твердого тела
добавим два мгновенных вращения с угловыми скоростями 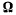и 
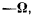линии действия которых проходят через точку 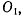Полученная новая система мгновенных движений твердого тела эквивалентна
первоначальной системе мгновенных движений. Но вектор 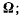проходящий через точку О и вектор 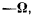, проходящий через точку 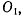и образуют пару вращений, эквивалентную мгновенно поступательному движению со скоростью
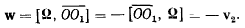
Результирующее движение состоит из одного мгновенного вращения с угловой скоростью 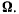линия действия которой проходит через точку 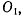и системы мгновенно-поступательных движений со скоростями 
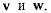Два последних мгновенно-поступательных движения эквивалентны одному мгновенно-поступательному движению со скоростью
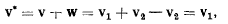
коллинеарной с линией действия вектора Мгновенное движение твердого тела, состоящее из таких мгновенно-вращательного и мгновенно-поступательного движений, у которых линии действия векторов мгновенно-угловой скорости и мгновенно-поступательной скорости коллинеарны, будем называть мгновенно-винтовым движением. Рассмотренное выше движение является мгновенно-винтовым движением твердого тела. Прямую линию твердого тела, для всех точек которой направление скорости совпадает с направлением мгновенно-угловой скорости твердого тела, будем называть винтовой осью. Отношение скорости поступательного движения тела вдоль винтовой оси к его угловой скорости
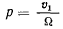
называют параметром винта. При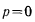 
будем иметь только
одно мгновенное вращение, при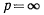 
мгновенно-поступательное движение. Мгновенно-винтовое движение определяет лишь состоя- состояние скоростей в данный момент времени, но не определяет полностью всего непрерывного движения твердого тела. Чтобы полностью определить движение, надо знать характер изменения скорости. Если же твердое тело действительно совершает винтовое движение, так что положение винтовой оси и параметры, определяющие состояние скоростей, не меняются, тогда за время 
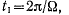т. е. за время одного полного оборота, тело продвинется вдоль винтовой оси на расстояние
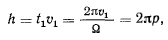
число h называют шагом винта.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
