Оглавление:
Теорема о сложении скоростей в сложном движении точки
Пусть некоторая неизменяемая система отсчета (в частном случае такой системой может быть абсолютно твердое тело S) совершает определенное движение относительно неподвижной системы координат 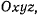 а материальная точка М движется относительно этой подвижной неизменяемой системы (рис. 36). Движение точки М по отношению к системе координат
а материальная точка М движется относительно этой подвижной неизменяемой системы (рис. 36). Движение точки М по отношению к системе координат 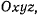 называют абсолютным движением, а ее траекторию в этом движении абсолютной траекторией. Движение точки относительно системы называют относительным движением, а траекторию в этом движении — относительной траекторией точки. Если точку М закрепить в некоторый момент в подвижной системе, то она будет двигаться лишь как точка подвижной системы.
называют абсолютным движением, а ее траекторию в этом движении абсолютной траекторией. Движение точки относительно системы называют относительным движением, а траекторию в этом движении — относительной траекторией точки. Если точку М закрепить в некоторый момент в подвижной системе, то она будет двигаться лишь как точка подвижной системы.
Такое движение точки называют переносным движением точки в данный момент времени. Соответствующая траектория точки называется переносной траекторией для данного момента времени. Скорость движения точки по абсолютной траектории называют абсолютной траекторией точки, а скорость движения точки по отношению к подвижной системе отсчета — ее относительной скоростью. Если точку в рассматриваемый момент времени закрепить в подвижной системе и рассматривать ее движение вместе с этой системой, то скорость ее движения в этот момент времени представит переносную скорость точки. Теорема. Абсолютная скорость материальной точки равна геометрической сумме ее переносной и относительной скоростей:
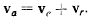
Доказательство. Рассмотрим два близких положения неизменяемой подвижной системы 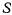 в моменты времени
в моменты времени 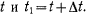 Перемещения точки в абсолютном, относительном и переносном движениях (рис. 36) представляются соответственно векторами
Перемещения точки в абсолютном, относительном и переносном движениях (рис. 36) представляются соответственно векторами 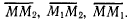 Вектор
Вектор 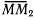 равен геометрической сумме векторов
равен геометрической сумме векторов 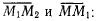
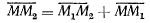
Средняя абсолютная скорость точки 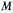 за время
за время 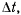 по
по
определению, равна отношению вектора перемещения ко времени 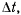 т. е.
т. е.
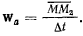
Разделив равенство (а) на 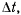 будем иметь
будем иметь
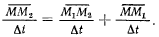
Вектор
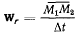
определяет среднюю скорость точки в подвижной системе S, вектор
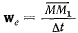
представляет среднюю скорость переносного движения, поэтому равенство можно переписать в виде
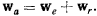
Векторы 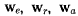 пропорциональны соответствующим векторам
пропорциональны соответствующим векторам
перемещений (рис. 36). В пределе при 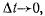 векторы
векторы 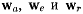 дают значения истинных скоростей в абсолютном, переносном и относительном движениях, т. е.
дают значения истинных скоростей в абсолютном, переносном и относительном движениях, т. е.
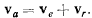
Полученная теорема имеет исключительно важное значение в механике. Рассмотрим некоторые примеры на ее применение.
Пример:
Палочка вращается в плоскости вокруг своего
неподвижного конца 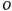 угловой скоростью
угловой скоростью 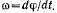 Точка
Точка 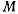 скользит вдоль палочки со скоростью
скользит вдоль палочки со скоростью 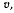 Определить абсолютную скорость точки (рис. 37).
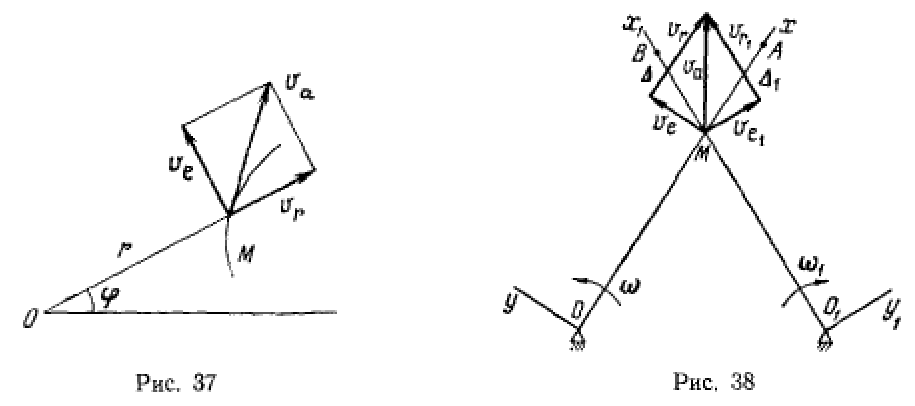
Определить абсолютную скорость точки (рис. 37).
Решение:
Точка участвует в двух движениях. Она перемещается вместе с палочкой и, кроме того, движется вдоль палочки. Относительно палочки точка совершает прямолинейное движение со скоростью 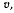 поэтому, приняв за подвижную
поэтому, приняв за подвижную
систему  палочку, получим следующее значение относительной
палочку, получим следующее значение относительной
скорости точки:
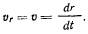
Для определения переносной скорости точки рассмотрим движение той точки палочки, которая в данный момент совпадает с движущейся материальной точкой. В переносном движении точка описывает окружность вокруг точки 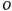 со скоростью
со скоростью 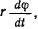 , а потому переносная скорость точки будет равна
, а потому переносная скорость точки будет равна
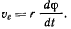
Так как векторы переносной и относительной скоростей ортогональны, будем иметь
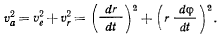
Полученные значения переносной и относительной скоростей совпадают с известными значениями радиальной и трансверсальной составляющими скорости.
Пример:
Палочки 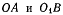 вращаются в плоскости чертежа с угловыми скоростями
вращаются в плоскости чертежа с угловыми скоростями 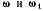 соответственно вокруг неподвижных точек
соответственно вокруг неподвижных точек 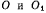 (рис. 38). На обе палочки одновременно надето кольцо
(рис. 38). На обе палочки одновременно надето кольцо 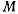 перемещающееся при вращении палочек. Определить абсолютную скорость кольца.
перемещающееся при вращении палочек. Определить абсолютную скорость кольца.
Решение:
Выберем подвижную систему 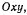 связанную с палочкой
связанную с палочкой 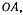 как указано на рис. 38. В этой системе кольцо все время находится на оси
как указано на рис. 38. В этой системе кольцо все время находится на оси 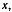 а его относительная скорость
а его относительная скорость 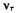 направлена вдоль выбранной оси, причем величина относительной скорости остается пока неизвестной. Переносная скорость
направлена вдоль выбранной оси, причем величина относительной скорости остается пока неизвестной. Переносная скорость 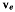 колечка равна скорости той точки подвижной системы (палочки
колечка равна скорости той точки подвижной системы (палочки 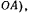 которая в данный момент совпадает с колечком. Обозначив через
которая в данный момент совпадает с колечком. Обозначив через 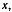 расстояние
расстояние 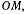 получим
получим
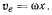
Эта скорость направлена параллельно оси 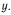 По теореме о сложении скоростей абсолютная скорость колечка равна геометрической сумме переносной и относительной скоростей
По теореме о сложении скоростей абсолютная скорость колечка равна геометрической сумме переносной и относительной скоростей
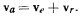
Конец вектора относительной скорости расположен на прямой 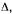 параллельной оси
параллельной оси 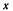 и проходящей через конец вектора переносной скорости. Следовательно, и конец вектора абсолютной скорости колечка будет находиться на прямой
и проходящей через конец вектора переносной скорости. Следовательно, и конец вектора абсолютной скорости колечка будет находиться на прямой 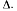 Выбирая теперь за подвижную систему оси
Выбирая теперь за подвижную систему оси 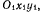 связанные с палочкой
связанные с палочкой 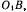
и повторяя все рассуждения, придем к заключению, что конец вектора абсолютной скорости будет находиться на прямой 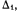 проходящей через конец вектора переносной скорости колечка
проходящей через конец вектора переносной скорости колечка 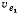 в системе
в системе 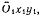 величина которой
величина которой 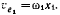 Точка пересечения прямых
Точка пересечения прямых 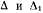 определяет положение конца вектора абсолютной скорости колечка.
определяет положение конца вектора абсолютной скорости колечка.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Движение точки по окружности |
| Проекции ускорения на оси естественного трехгранника |
| Метод Роберваля построения касательных к плоским кривым |
| Аналитическое доказательство теоремы о сложении скоростей |

