Движение точки по окружности
Рассмотрим задачу о движении
точки по окружности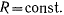 
Из формул для радиальной и трансвер-сальной составляющих ускорения получим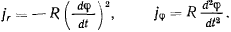 
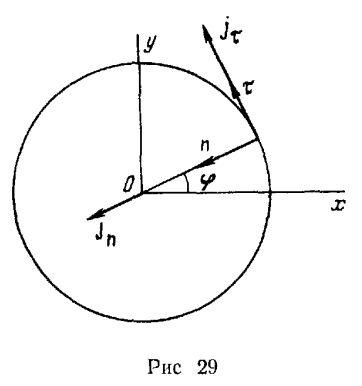
Здесь радиальная составляющая направлена к центру окружности, а трансверсальная составляющая — по касательной к окружности. Обозначим через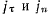 
проекции ускорения точки на касательную и нормаль к окружности. Будем иметь (рис. 29)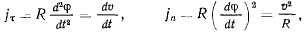 
где
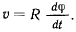
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Ускорение точки |
| Скорость и ускорение точки в полярных координатах |
| Проекции ускорения на оси естественного трехгранника |
| Теорема о сложении скоростей в сложном движении точки |
