Оглавление:
Скорость и ускорение точки в полярных координатах
Пусть точка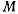 
совершает движение в плоскости 
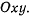При помощи формул преобразования перейдем от декартовых координат 
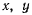к полярным координатам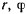 
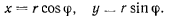
При движении точки М величины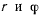 
будут некоторыми функциями времени. Тогда проекции скорости на декартовы оси координат получим из соотношений
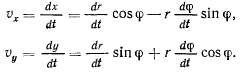
Введем два ортогональных направления: направление из начала
координат на движущуюся точку — радиальное и перпендикулярное к нему направление в сторону возрастания угла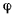 
трансверсальное направление. Легко подсчитать проекции
вектора скорости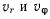 
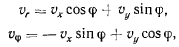
после подстановки сюда значений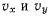 
будем иметь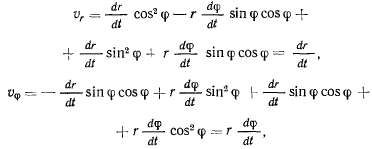 
т.е.
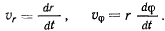
Эти проекции называют радиальной и трансверсальной составляющими скорости точки. Рассмотрим проекции ускорения точки на оси декартовой системы координат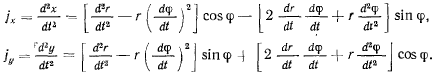 
Проектируя ускорение точки на радиальное и трансверсальное направления, получим
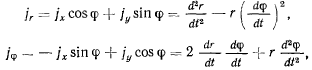
т. е.
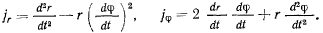
Эти проекции называются радиальной и трансверсальной составляющими ускорения. Как нетрудно заметить, эти составляющие не являются непосредственными производными от радиальной и трансверсальной составляющих скорости точки.
Пример:
Определить траекторию, скорость и ускорение точки,
движение которой в плоскости задано в полярных координатах: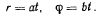 
Решение:
Исключив время, найдем траекторию точки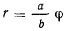 
(архимедова спираль), а затем определим скорость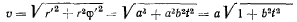 
и ускорение
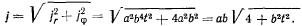
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Кинематика точки |
| Ускорение точки |
| Движение точки по окружности |
| Проекции ускорения на оси естественного трехгранника |
