Груз массой т = 1,5 т при помощи троса поднимается на высоту Н = 30 м.

Пример задачи 10.1

Груз массой т = 1,5 т при помощи троса поднимается на высоту Н = 30 м (рис. 10.2). В первые три секунды подъема с постоянным ускорением груз проходит путь s = 22,5 м.

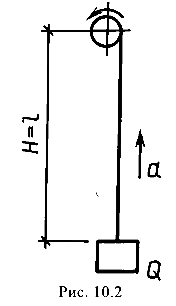
Определить площадь сечения троса, если его расчетное сопротивление R = 190 МПа, модуль продольной упругости Е = 100 ГПа, объемная плотность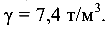

Задачу решить без и с учетом массы троса.

Решение

В момент разгона ускорение подъема груза составляет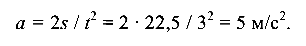

Приведем данные в единицы, требуемые системой СИ: вес груза

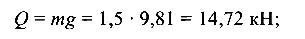
плотность троса

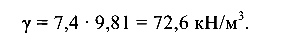
Решение без учета массы троса.

Усилие в тросе от статического действия груза

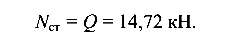
Динамический коэффициент по формуле (10.1)

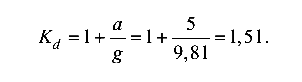
Усилие в тросе от динамического действия груза

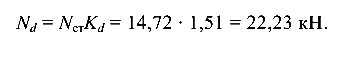
Условие прочности троса

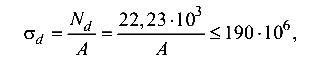
откуда площадь сечения троса

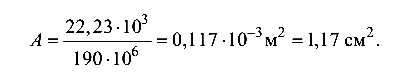
Определим максимальное напряжение в тросе с учетом его массы. Вес троса

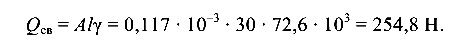
Статическое усилие в тросе

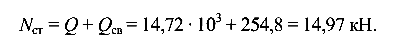
Динамическое усилие в тросе

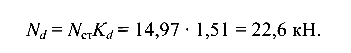
Динамическое напряжение в тросе

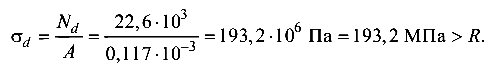
Перенапряжение составляет 1,68 %, что допустимо. Заметим, что влияние массы троса на напряжение в нем в данном случае незначительное (небольшая длина троса). Вычислим удлинение троса. Удлинение от статического действия груза

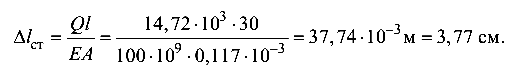
Удлинение от динамического воздействия груза

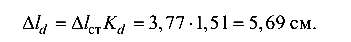
Решение с учетом массы троса

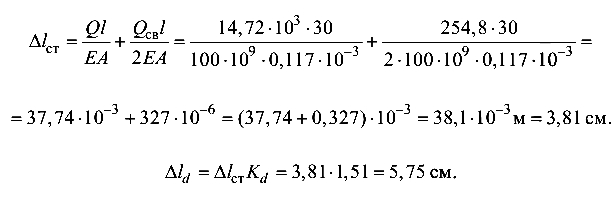
Учет массы троса показал незначительное увеличение удлинения (на 1,05 %). Поэтому при небольшой длине троса его собственным весом при вычислении напряжений и деформаций можно пренебречь.

Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:

Примеры решения задач по сопротивлению материалов

Дополнительные задачи которые вам будут полезны:

Пример задачи 9.1 Стальная стойка квадратного поперечного сечения (а = 7 см) длиной l = 3м центрально нагружена сжимающей силой F(рис. 9.4, а). Нижний конец стойки защемлен, а верхний в направлении главной центральной оси Х — защемлен, в направлении оси Y — свободен. Определить наибольшее допустимое значение силы F, если R = 210 МПа, Е = 200 ГПа, а коэффициент запаса устойчивости

Пример задачи 9.8 Деревянная консольная балка длиной l = 2 м прямоугольного поперечного сечения нагружена сосредоточенной силой F = 5 кН в точке К под углом к оси Z (рис. 9.12, а). Проверить прочность и устойчивость балки.

Пример задачи 10.4 На стальной стержень длиной l = 1 м квадратного поперечного сечения (а = 5 см), рис. 10.7, с высоты Н = 10 см падает груз массой т = 30,6 кг. Проверить прочность стержня без и с учетом его массы, если допускаемое напряжение из расчета на устойчивость составляет R = 74,1 МПа.

Пример задачи 10.7 Электродвигатель весом Q = 1,5 кН установлен на консольных деревянных балках прямоугольного поперечного сечения при соотношении сторон h / b= 1,5 (рис. 10.12, а).