Пример задачи 1.1
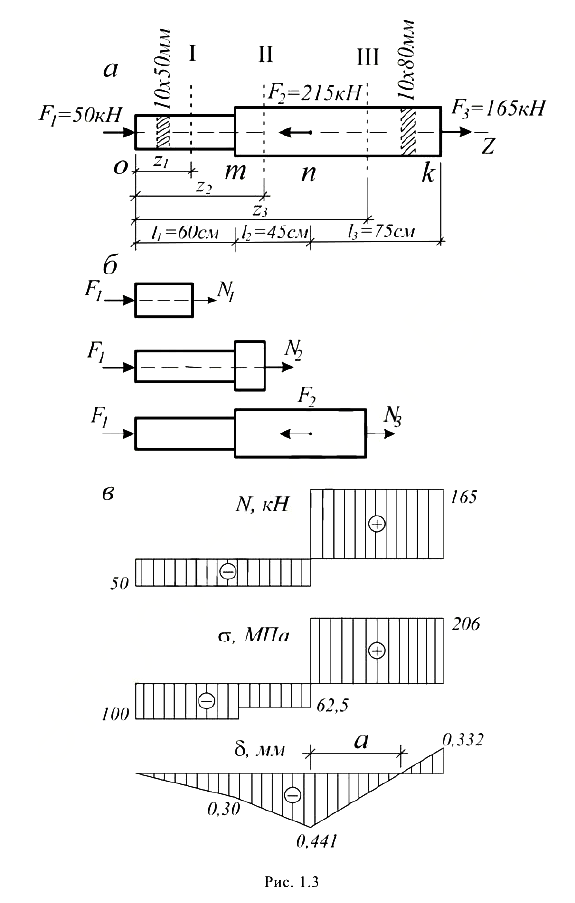
Стальная полоса прямоугольного поперечного сечения нагружена системой расчетных сил F (рис. 1.3, а).
Проверить прочность и жесткость полосы.
Для стали: расчетное сопротивление R = 210 МПа, модуль продольной упругости Е = 200 ГПа, допустимая относительная продольная деформация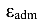 
= 1,05-10 3.
Решение
Нагрузка F, действующая по продольной оси полосы, вызывает в ней деформацию растяжения-сжатия.
Проверим, выполняется ли условие равновесия элемента конструкции:
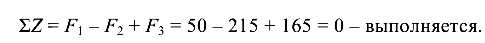
На рассматриваемой полосе выделяются три расчетных участка, в пределах которых намечаются сечения I-III. Длинам участков l придается индекс номера участка.
Для определения продольных сил N на участках элемента воспользуемся первым приемом. Для этого нужно составить расчетные схемы для всех «отсеченных» участков элемента, начиная, например, с левого конца (рис. 1.3, б), и записать для них условия равновесия.
Рекомендуется искомые продольные силы N направлять от рассматриваемого сечения, т. е. считать положительными. Участок I:
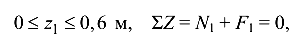
откуда
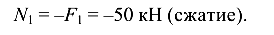
Участок II:
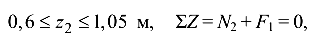
откуда
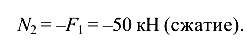
Участок III:
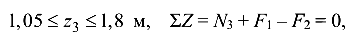
откуда
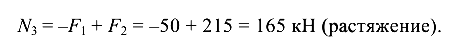
По полученным значениям N в выбранном масштабе строится эпюра продольных сил — эпюра N (рис. 1.3, в). Положительные значения N откладываются вверх от линии эпюры, а отрицательные — вниз.
Заметим, что в пределах расчетных участков N = const. В сечении, где приложена сосредоточенная сила F, на эпюре N имеется «скачок» на величину этой силы (165 + 50 = 215 кН). Из эпюры N следует, что наиболее нагруженным является третий участок: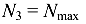 
Нормальные напряжения, возникающие в поперечных сечениях на расчетных участках элемента, определяются по формуле (1.1).
Сечение I:
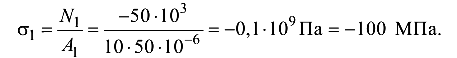
Сечение II:
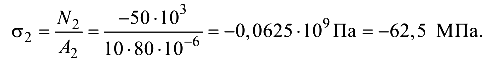
Сечение III:
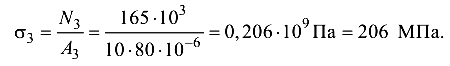
Значения нагрузки и геометрические размеры элемента конструкции могут быть заданы в любых соответствующих единицах (Н, кН, МН, мм, см, м). В формулы напряжений и деформаций они должны подставляться в ньютонах и метрах.
По полученным значениям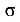
строится эпюра нормальных напряжений (рис. 1.3, г). Правило построения такое же, как и для эпюры N. В пределах расчетных участков 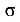= const, так как N = const и А = const. В сечении, где приложены сосредоточенные силы F, а также где изменяются размеры поперечного сечения, на эпюре 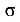наблюдается «скачок». Из эпюры а следует, что наиболее напряженным является третий участок: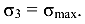
Проверка прочности выполняется по условию прочности (1.2). Наибольшее нормальное напряжение возникает на третьем расчетном участке.
Так как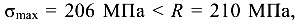 
прочность элемента по нормальным напряжениям обеспечена.
Для проверки жесткости вначале по формуле (1.3) определим значения абсолютной продольной деформации на участках элемента.
Участок I:
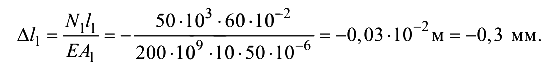
Участок II:
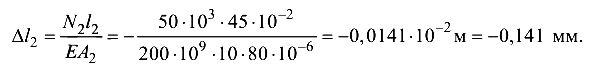
Участок III:
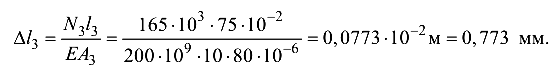
Значения относительной продольной деформации на участках элемента вычислим по формуле (1.5):
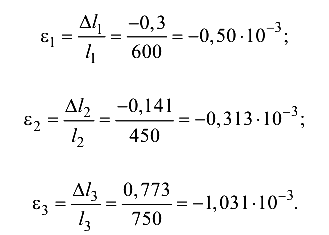
Условие жесткости элемента конструкции выполняется, так как
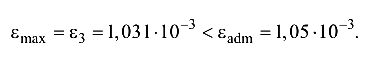
Перемещения характерных сечений (о-k, где изменяются А или N) вычисляются исходя из значений деформаций отдельных участков элемента. Крайнее левое сечение примем за относительно неподвижное: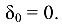 
Перемещения других сечений находятся последовательным добавлением к предыдущему перемещению деформаций последующих участков:
Эпюра перемещений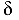 
показана на рис. 1.3, д. На третьем участке эпюра 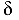пересекает ось. Определим положение сечения и, в котором перемещение равно нулю:
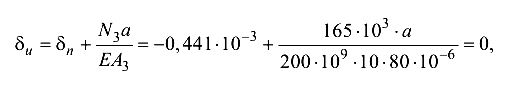
откуда а = 0,428 м = 42,8 см.
Из эпюры 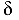следует, что наибольшее перемещение претерпевает сечение 
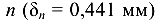в сторону крайнего левого (о). Перемещение правого концевого сечения (k) по отношению к крайнему левому (о) составляет 
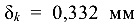и направлено в положительном направлении оси Z.
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
