Метод Эйлера определения критической сжимающей силы для стержня
Леонард Эйлер (нем. Leonhard Euler; 4 (15) апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург, Российская империя) — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
При малой сжимающей силы 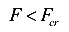 прямолинейный стержень находится в состоянии устойчивого равновесия. Такое состояние только одно — прямолинейная форма (случай 1).
прямолинейный стержень находится в состоянии устойчивого равновесия. Такое состояние только одно — прямолинейная форма (случай 1).
При большой сжимающей силе 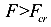 прямолинейный стержень находится в состоянии неустойчивого равновесия. Такое состояние может быть только одно — прямолинейна форма (случай 3).
прямолинейный стержень находится в состоянии неустойчивого равновесия. Такое состояние может быть только одно — прямолинейна форма (случай 3).
Но имеется граничное состояние, когда 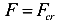 . В этом случае сжимаемый стержень находится в безразличном состоянии равновесия. Прямолинейная форма равновесия сжатого стержня в этом случае не является единственной. Форм равновесия становится бесконечное множество. При этом и незначительно искривленные стержни тоже будут
. В этом случае сжимаемый стержень находится в безразличном состоянии равновесия. Прямолинейная форма равновесия сжатого стержня в этом случае не является единственной. Форм равновесия становится бесконечное множество. При этом и незначительно искривленные стержни тоже будут
находиться в состоянии равновесия. То есть происходит бифуркация форм равновесия (случай 2).
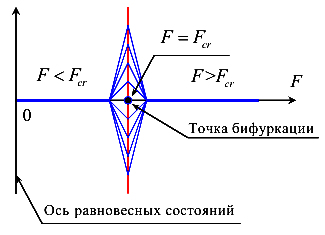
Согласно определению Эйлера — наименьшее значение сжимающей силы, при которой происходит разветвление форм равновесия, называется критической силой.
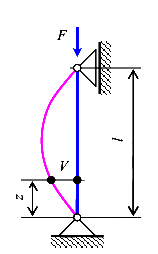
Рассмотрим сжатый прямолинейный стержень.Изгибающий момент от продольной силы равен
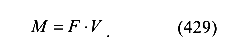
Дифференциальное уравнение изгиба имеет вид
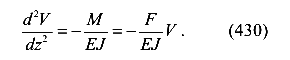
Для удобства обозначим
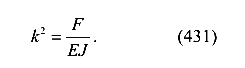
Тогда

Решение дифференциального уравнения(432) имеет вид
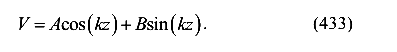
Подставим решение (452) в уравнение (451) и убедимся, что оно удовлетворяется.
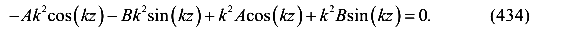
Для определения коэффициентов А и В воспользуемся граничными условиями при z = 0; V = 0.
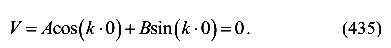
Отсюда имеем значение А=0.
Следовательно, решение уравнения можно выразить более просто

То есть, стержень в момент потери устойчивости искривляется по синусоиде, при z =l; V = 0

Требуется определить, при каких условиях решение (437) возможно. Если В = 0, то стержень не искривляется. Этот случай не рассматривается, так как противоречит условию задачи. Поэтому

Это условие выполняется при
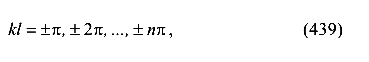
где n — числа натурального ряда.
Учитывая выражение для k, получим форму искривления сжатого стержня и выражение для критической силы. Рассмотрим только положительные значения и выразим значение критической силы согласно принятому решению.

При 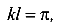
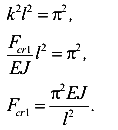
В этом случае стержень в момент потери устойчивости принимает форму одной полуволны синусоиды (рис. 134).

При 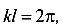 ,
,
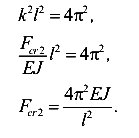
В этом случае стержень в момент потери устойчивости принимает форму двух
полуволн синусоиды (рис. 135). И так далее…..
Для реального стержня следует принимать во внимание только минимальную критическую силу
Формула Эйлера опубликована в 1744 г. Формула Эйлера справедлива только в случае упругой деформации материала стержня, так как при ее выводе используется дифференциальное уравнение упругой оси стержня при изгибе.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Устойчивость сжатых стержней |
| Основные понятия об устойчивости |
| Влияние способов закрепления сжатого стержня на величину критической силы |
| Пределы применимости формулы Эйлера. Формула Ясинского |

