Определение положения нейтральной оси при косом изгибе
Рассмотрим сечение прямоугольной формы (рис. 113). Так как это сечение имеет оси симметрии, поэтому известно положение его главных центральный осей инерции — это сами оси симметрии.
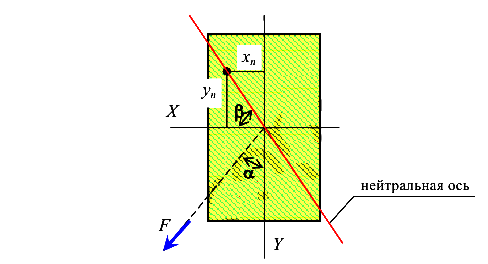
при косом изгибе
Линия, в каждой точке которой напряжения равны нулю, называется нейтральной линией (осью).
Пусть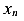 
, 
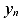координаты точки, расположенной на нейтральной линии. При этом поставим условие, чтобы они не были равными нулю. В соответствии с определением нейтральной оси, поставим условие, чтобы нормальной напряжение в этой точке было равно нулю.
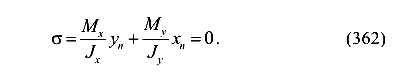
Так как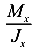 
, 
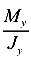не зависят от координат точек сечения, то отсюда следует, что нейтральная линия — это прямая (381). Значит, ее можно называть нейтральной осью.
Разделим обе части уравнения (381) на ,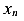 
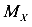и умножим на 
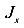. В результате получим уравнение (382)
Перенесем второе слагаемое на правую сторону уравнения (363) и получим
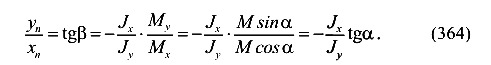
Без учета знака получим
Из формулы (362), очевидно, что напряжение в центре тяжести сечения, то есть пр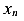и и 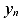равным нулю, при косом изгибе равно нулю. Следовательно, нейтральная линия (ось) при косом изгибе всегда проходит через центр тяжести сечения, и наклонена к оси X под углом 
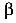(365).
Угол 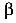всегда откладываем от оси X так, чтобы нейтральная ось проходила через отрицательные квадранты, если оси Х и У направлять в сторону растянутых волокон.
Если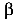 
то, очевидно, что нейтральная ось не перпендикулярна силовой линии, то есть плоскости суммарного изгибающего момента, так как 
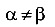. Отметим, что плоскость суммарного изгибающего момента в сечении наклонена к оси У под углом 
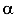(рис.113).
Для сечений, у которых=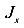 
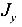(круг, квадрат, кольцо и др.) косой изгиб, согласно данному определению, вообще невозможен, так как любая центральная ось сечения является главной. Поэтому силовая плоскость будет всегда содержать одну из многочисленных главных осей инерции. Такой изгиб следует называть не косым изгибом, а изгибом в двух плоскостях.
Рассмотрим частный случай косого изгиба.
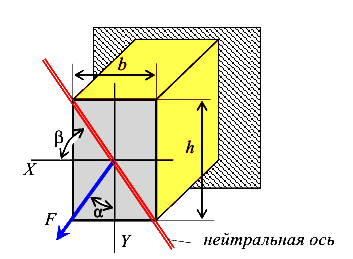
Дана балка прямоугольного сечения (рис.114). Пусть силовая плоскость проходит через диагональ сечения.
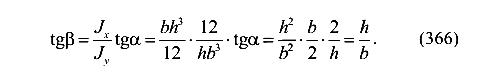
Таким образом, нейтральная ось совпадает с другой диагональю сечения.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Косой изгиб. Общие понятия |
| Определение напряжений при косом изгибе |
| Определение прогибов балки при плоском и пространственном косых изгибах |
| Построение эпюр внутренних сил при косом изгибе балки |
