Определение напряжений при косом изгибе
Пусть дана консольная балка прямоугольного сечения, загруженная на конце сосредоточенной силой F (рис.111).
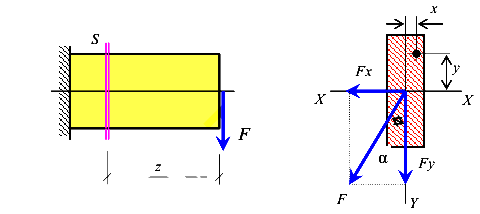
Разложим силу F на составляющие по направлению оси X и оси У, являющимися главными осями инерции рассматриваемого сечения в связи с тем, что они являются осями симметрии сечения.
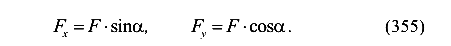
Каждая из составляющих сил вызывает в сечении S изгибающий момент
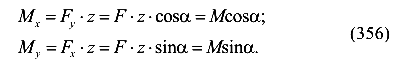
Таким образом, при косом изгибе в одном сечении действуют два изгибающих момента — момент относительно оси X и момент относительно оси У. Учитывая принцип независимости действия сил, определим нормальное напряжение в произвольной точке поперечного сечения
или
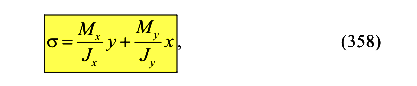
где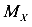 
, 
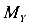— изгибающие моменты в сечении относительно главных осей инерции Х и У
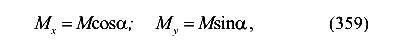
где
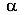— угол между плоскостью суммарного изгибающего момента и осью У;
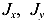— главные центральные моменты инерции рассматриваемого сечения;- х,у — координаты точки, в которой вычисляется напряжение.
Для получения правильного знака оси X и У следует направлять в сторону растянутых волокон, изгибающие моменты 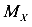и 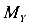всегда принимать положительными, а координаты х и у со своим знаком.
Если сечение имеет точку одновременно максимально удаленную от осей X и У, то максимальные напряжения могут быть найдены по упрощенной формуле
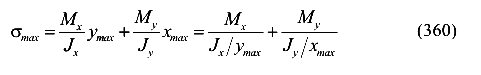
или
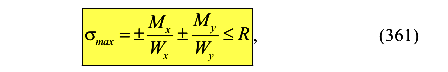
где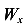 
, 
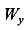— осевые моменты сопротивления сечения относительно осей X и У.
Примеры таких сечений приведены на рисунке (рис. 112)
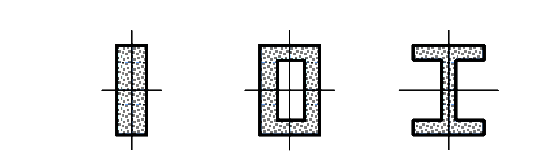
двутавровое
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Сложное сопротивление |
| Косой изгиб. Общие понятия |
| Определение положения нейтральной оси при косом изгибе |
| Определение прогибов балки при плоском и пространственном косых изгибах |
