Теорема о взаимности работ внутренних сил
Пусть к балке (рис. 98) приложена сила 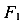 которая вызывает в сечении изгибающий момент
которая вызывает в сечении изгибающий момент 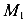 . Приложим к балке еще и силу
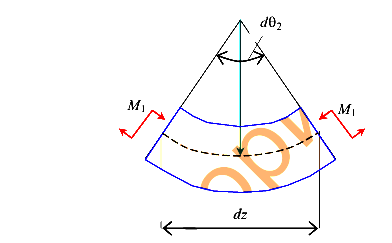
. Приложим к балке еще и силу 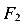 , которая вызвала дополнительный угол поворота сечений на участке dz равный
, которая вызвала дополнительный угол поворота сечений на участке dz равный 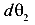 .
.
Виртуальная работа внутренних сил от 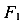 , на перемещениях, вызванных силой
, на перемещениях, вызванных силой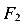 равна
равна

Здесь

Кривизна участка балки равна

Отсюда имеем
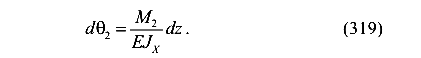
Подставим выражение (319) в формулу (316) и получим виртуальную работу внутренних сил на элементарном участке балки
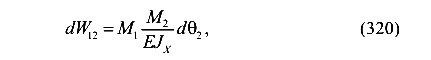
где 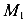 ,
,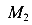 — функции изгибающих моментов от сил
— функции изгибающих моментов от сил 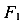 , и
, и 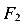 . Виртуальная работа по всей длине балки равна интегралу
. Виртуальная работа по всей длине балки равна интегралу

Аналогично

Отсюда, очевидно, что

Сформулируем теорему о взаимности работ внутренних сил.
Работа внутренних сил первого состояния на перемещениях второго состояния равна работе внутренних сил второго состояния на перемещениях первого состояния.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Расчет статически неопределимых стержневых систем |
| Теорема о взаимности работ внешних сил |
| Теорема о взаимности перемещений |
| Определение перемещений методом Максвелла-Мора |

