Теорема о взаимности работ внешних сил
Эта теорема впервые опубликована итальянским ученым Бетти (1823-1892 гг) и названа его именем.
Рассмотрим два состояния балки
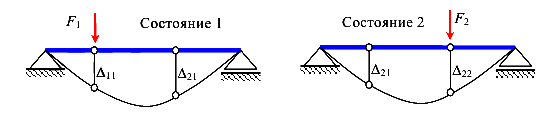
Поясним обозначения. Первый индекс обозначает направление перемещения, а второй — фактор, вызывающий это перемещение.
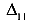 — перемещение по направлению первой силы от действия первой силы;
— перемещение по направлению первой силы от действия первой силы;-
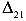 — перемещение по направлению второй силы от действия первой силы;
— перемещение по направлению второй силы от действия первой силы; -
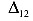 — перемещение по направлению первой силы от действия второй силы;
— перемещение по направлению первой силы от действия второй силы; 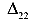 перемещение по направлению второй силы от действия второй силы.
перемещение по направлению второй силы от действия второй силы.
Рассмотрим деформации балки при разных последовательностях приложения сил (рис.97).
Первый вариант загружения (рис. 97, а) — вначале прикладываем силу 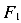 потом силу
потом силу 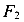 .
.
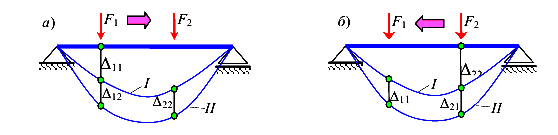
После загрузки балки первой силой она искривляется (по линии I). При этом образуется прогиб 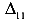 . Затем прикладываем вторую силу. Балка еще больше искривляется (по линии II) и появляются дополнительные прогибы
. Затем прикладываем вторую силу. Балка еще больше искривляется (по линии II) и появляются дополнительные прогибы 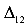 и
и 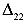 . Работа, совершенная этими силами, равна
. Работа, совершенная этими силами, равна
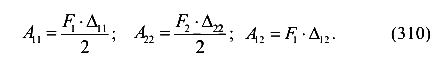
Суммарная работа равна

Здесь 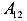 — возможная (виртуальная) работа первой силы.
— возможная (виртуальная) работа первой силы.
Второй вариант загружения (рис. 97, б) — вначале прикладываем силу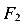 потом силу
потом силу 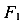 .
.
После загрузки балки второй силой она искривляется (по линии I). При этом образуется прогиб 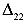 . Затем прикладываем вторую силу. Балка еще больше искривляется (по линии II). Появляются дополнительные прогибы
. Затем прикладываем вторую силу. Балка еще больше искривляется (по линии II). Появляются дополнительные прогибы 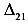 и
и 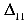 . Работа, совершенная силами, равна
. Работа, совершенная силами, равна
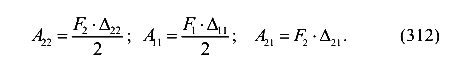
Суммарная работа равна

Здесь 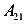 — возможная (виртуальная) работа второй силы.
— возможная (виртуальная) работа второй силы.
Мы знаем, что работа, совершенная системой сил не зависит от порядка их приложения.

Поэтому, сравнивая выражения (310) и (313), приходим к выводу, что

Сформулируем теорему о взаимности внешних сил.
Работа внешних сил первого состояния на перемещениях второго состояния равна работе внешних сил второго состояния на перемещениях первого состояния.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:

