Расчет статически неопределимых стержневых систем
Ограничимся рассмотрением стержневых систем, содержащих абсолютно жесткий брус (диск), прикрепленный к шарнирной неподвижной опоре (рис. 93). Такое условие необходимо для упрощения расчета механической системы.
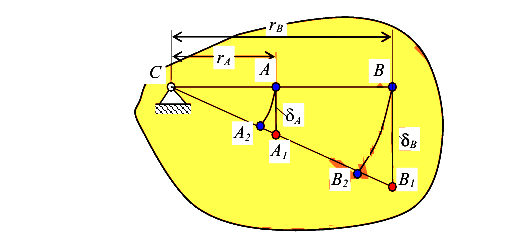
Отметим некоторые особенности перемещений точек и деформаций элементов таких систем:
- абсолютно жесткий диск не деформируется, то есть расстояние между любыми двумя его точками остается неизменным;
- перемещение точки диска при его повороте прямо пропорционально ее удаленности от центра поворота;
- любая точка диска, исключая точку закрепления, при его повороте перемещается по дуге окружности с центром в шарнире С;
- из-за малости перемещения дугу окружности заменяют касательной. Учитывая перечисленные особенности и рисунок, получим равенства, основанные на пропорциях отрезков
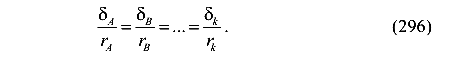
Рассмотрим порядок расчета таких систем на примере в общем виде (рис. 94
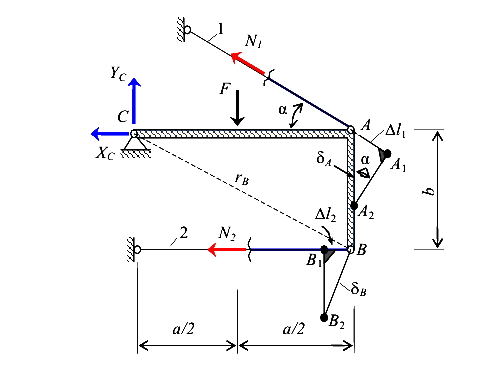
Вначале установим степень статической неопределимости системы.
Число неизвестных равно 4 — 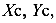
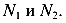
Число линейно независимых уравнений равно 3 —
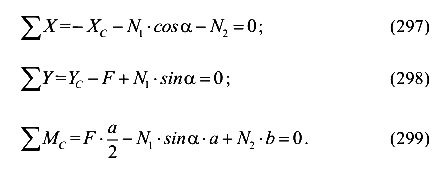
Таким образом, система один раз (однажды) статически неопределимая.

Требуется составить одно дополнительное уравнение. Это уравнение получаем на основе деформированной схемы системы.
Радиусы окружностей, по которым движутся ключевые точки А и В равны
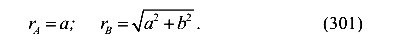
Отношение перемещений ключевых точек А и В равно отношению радиусов тех окружностей, которые они описывают

Отсюда имеем

или

Полученное последнее выражение (304) называют уравнением совместности перемещений. Отметим, что отношение перемещений точек А и В всегда будет одинаковым независимо от того, какие нагрузки будут приложены к стержневой системе. Это отношение зависит только от положения этих точек.
Установим связь между перемещениями и деформациями.
Из треугольника 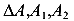 (рис.94) выразим перемещение точки А через деформацию первого стержня
(рис.94) выразим перемещение точки А через деформацию первого стержня

Из подобия треугольников 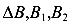 и
и 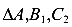 получим пропорцию
получим пропорцию

Минус ставим по тому, что на схеме деформаций второй стержень имеет отрицательную деформацию, то есть укорачивается. Отсюда получим
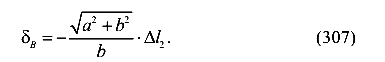
Найденные выражения (305) и (307) подставим в уравнение совместности перемещений (304). В результате получим уравнение совместности деформаций.

Учитываем закон Гука и получим
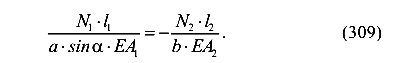
Присоединим полученное дополнительное уравнение к трем уравнениям равновесия (297), (298) и (299) и получим четыре уравнения с четырьмя неизвестными. Решив эту систему, получим значения всех неизвестных — 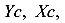
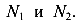 Этот этап расчета системы называется раскрытием статической неопределимости. Дальнейший расчет выполняется так же, как и для статически определимых систем.
Этот этап расчета системы называется раскрытием статической неопределимости. Дальнейший расчет выполняется так же, как и для статически определимых систем.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:

