Определение касательных напряжений при кручении сечений круглого (кольцевого) сечений
Рассмотрим элементарный участок стержня круглого сечения, подвергнутого кручению (рис. 79).
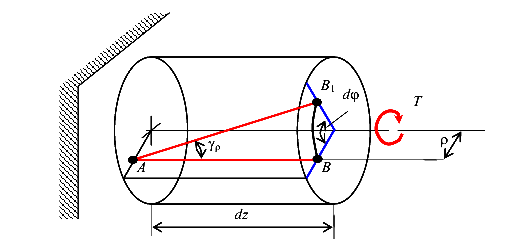
Рассмотрим продольное волокно, взятое на расстоянии 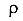 от оси стержня. Угол наклона (угол сдвига) волокна равен
от оси стержня. Угол наклона (угол сдвига) волокна равен
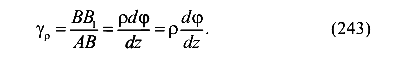
Воспользуемся законом Гука при сдвиге
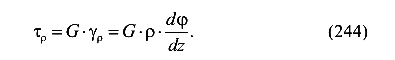
Следовательно, касательное напряжение в стержне круглого поперечного сечения при его кручении прямо пропорционально расстоянию от оси стержня до точки, где вычисляется напряжение. При этом, очевидно, что наибольшие напряжения появляются в точках поверхности стержня (рис. 80).
Отсюда имеем

Установим связь между касательным напряжением и крутящим моментом.
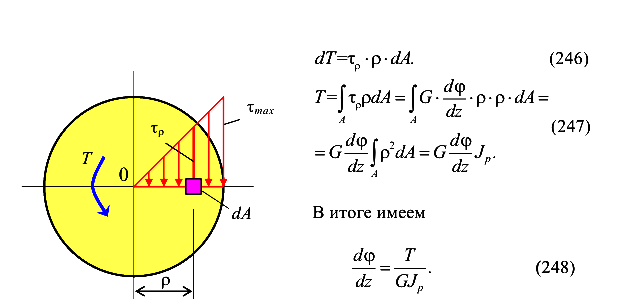
В уравнениях (245) и (248) левые части раны, поэтому будут равны и правые части

Отсюда имеем формулу для вычисления касательного напряжения при кручении в произвольной точке поперечного сечения

где
- Т— крутящий момент в рассматриваемом сечении;
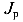 — полярный момент инерции круглого или кольцевого сечения. Для круглого сечения полярный момент вычисляется по формуле
— полярный момент инерции круглого или кольцевого сечения. Для круглого сечения полярный момент вычисляется по формуле

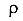 — расстояние от точки, где вычисляется касательное напряжение, до оси стержня.
— расстояние от точки, где вычисляется касательное напряжение, до оси стержня.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:

