Оглавление:
Метод непосредственного интегрирования
Метод основан на непосредственном интегрировании полученного приближенного дифференциального уравнения. Последовательно интегрируем дифференциальное уравнение (163). Вначале запишем его так
Учитываем, что первая производная от прогиба является функцией угла поворота поперечных сечений
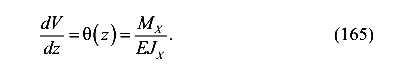
Подставляем выражение (165) в уравнение (164) и получим
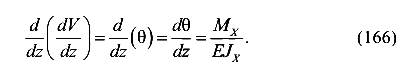
Разделим дифференциалы
Проинтегрируем левую и правую части уравнения (167)
Выразим угол поворота через прогибы
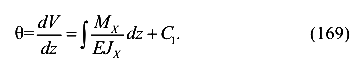
Разделим дифференциалы
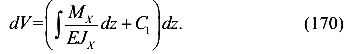
Проинтегрируем левую и правую части уравнения и получим решение
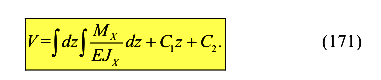
Постоянные интегрирования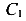 
и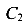 
определяются из граничных условий на концах каждого участка балки. Число постоянных интегрирования равно удвоенному числу участков на балке. В этом недостаток рассматриваемого метода. Достоинством метода является возможность определения углов поворота и прогибов балки переменной жесткости и при любой по сложности нагрузке.
Пример:
Определение прогиба и угла поворота сечения балки методом непосредственного интегрирования. Рассмотрим защемленную балку постоянной жесткости (рис.63).
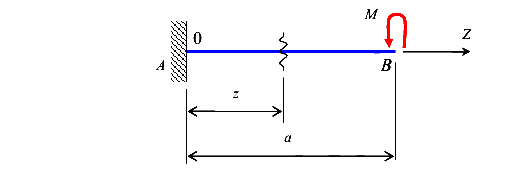
Изгибающий момент выражается функцией
Угол поворота
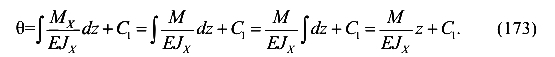
Прогиб
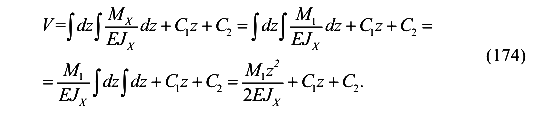
Определим постоянные интегрирования. Для этого используем условие на концах балки:
1) при z = 0,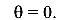 
2) при z = 0, V=0.
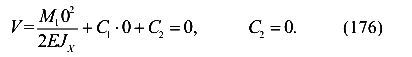
В результате получим аналитические выражения (функции) для углов поворота и прогибов балки.
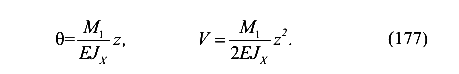
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
