Пример решения задачи №92.
Одним из компонентов топлива в двигателе ракеты является жидкий водород, плотность которого в момент закипания 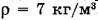 . Определить среднюю длину свободного пробега молекул водорода
. Определить среднюю длину свободного пробега молекул водорода 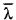 при этом, если эффективный диаметр молекулы водорода
при этом, если эффективный диаметр молекулы водорода 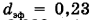 нм (нанометров). Молярная масса водорода М = 0,002 кг/моль. Газ считать идеальным.
нм (нанометров). Молярная масса водорода М = 0,002 кг/моль. Газ считать идеальным.
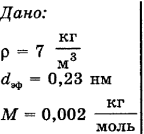
Решение:
Средняя длина свободного пробега молекул определяется формулой
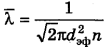 , где n — концентрация молекул водорода.
, где n — концентрация молекул водорода.
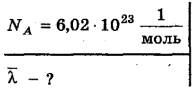
Концентрацию молекул, т. е. их число в единице объема, можно «связать» с плотностью р, разделив плотность р (т. е. массу всех молекул в единицу объема) на массу одной молекулы водорода 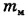 . Очевидно, что при этом мы найдем число молекул в единице объема, т. е. их концентрацию
. Очевидно, что при этом мы найдем число молекул в единице объема, т. е. их концентрацию 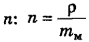 , где
, где 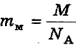 .
.
Тогда 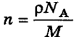 и
и
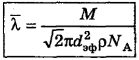
Задача в общем виде решена. Переведем все единицы в СИ. При этом учтем, что 1 нм (нанометр) = 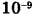 м, поэтому
м, поэтому 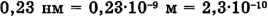 .
.
Подставим числа и произведем вычисления:
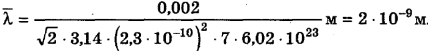
Ответ: 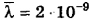 .
.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:

