Пример решения задачи №82.
Определить минимальную мощность насоса N, поднимающего воду по трубе на высоту Н = 10 м, если площадь поперечного сечения трубы 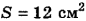 и за каждую
и за каждую  с насос поднимает
с насос поднимает 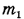 = 8 кг воды. Плотность воды
= 8 кг воды. Плотность воды 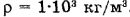 .
.
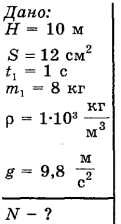
Решение:
Минимальную мощность насоса N определим отношением работы А по подъему некоторой массы воды m ко времени t, за которое эта работа совершена: 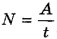
Совершенная насосом работа равна изменению энергии воды, заполнившей трубу, по сравнению с энергией, которой вода обладала до подъема.
Но, поскольку до подъема вода покоилась, то там ее кинетическая энергия была равна нулю, а за нулевой уровень потенциальной энергии тоже можно принять уровень, на котором вода покоилась, и тогда энергия воды там будет равна нулю. Поэтому совершенная работа будет равна полной механической энергии Е воды массой m, заполнившей трубу: А = Е, и тогда 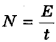 . (1)
. (1)
Полная механическая энергия воды в трубе Е складывается из ее кинетической 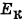 и потенциальной
и потенциальной 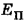 энергий:
энергий:
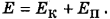
Кинетическая энергия воды 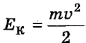
где v — скорость течения воды в трубе (будем считать ее постоянной).
Скорость и можно определить отношением пути l, пройденного элементом воды за время 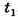 к этому промежутку времени:
к этому промежутку времени: 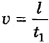 , где за путь I можно принять длину элемента воды массой ту.
, где за путь I можно принять длину элемента воды массой ту. 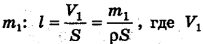 — объем воды массой
— объем воды массой 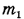 .
.
Поэтому 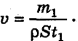
Масса воды m, поднятая за время t, может быть определена произведением массы воды, поднятой за единицу времени 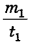 , на время
, на время 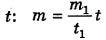 .
.
Подставим (4) и (5) в (3): 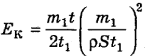
Потенциальная энергия 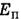 центра масс столба воды массой m будет:
центра масс столба воды массой m будет: 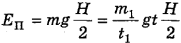 . (7)
. (7)
Подставим (6) и (7) в (2):
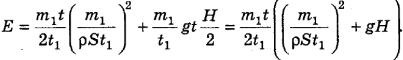
Нам осталось подставить (8) в (1), и задача будет решена:
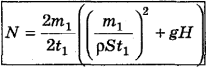
Время t при подстановке сократилось. Переведем в СИ единицу площади:
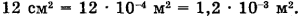
Произведем вычисления:
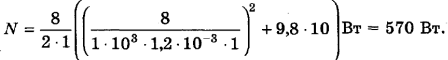
Ответ: 570 Вт.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:

