Оглавление:
Пример решения задачи №62.
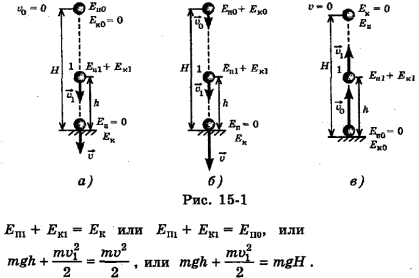
Тело массой т падает свободно на землю с высоты Н без начальной скорости (рис. 15-1, а).
Потенциальная энергия тела на высоте 
полностью превращается в его кинетическую энергию у земли: 
,
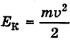где у — скорость тела у земли. Приравняв правые части этих равенств, мы можем определить искомую величину, если остальные известны: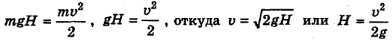 
.
В некоторой промежуточной точке 1 на высоте h сумма потенциальной энергии тела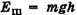 
и кинетической энергии 
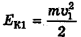равна его кинетической энергии у земли 
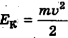или потенциальной энергии на высоте 
:
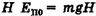Таким образом, полная механическая энергия этого тела Е в любой точке падения одна и та же:
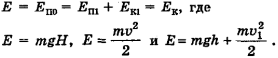
Дополнительный пример:
Тело брошено вниз с высоты Н с начальной скоростью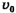 
и у земли набрало скорость v (рис. 15-1, б). Теперь на высоте Н у тела есть как потенциальная энергия 
, так и кинетическая энергия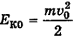 
, поэтому у земли кинетическая энергия тела 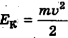будет равна сумме начальных кинетической и потенциальной энергий тела на высоте H:
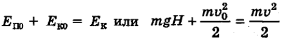, а в промежуточной точке 1: 
, 
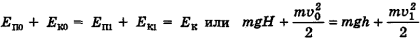В зависимости от условия задачи можно применить любое из этих уравнений.
Дополнительный пример:
Тело брошено с земли вверх с начальной скоростью 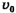(рис. 15-1, в), его начальная потенциальная энергия на земле равна нулю, а начальная кинетическая энергия тела на земле максимальна 
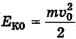При взлете тела на максимальную высоту Н его кинетическая энергия полностью превращается в потенциальную энергию 
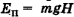, а в любой промежуточной точке 1 сумма потенциальной 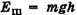и кинетической 
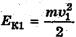энергий тела равна начальной кинетической 
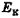или конечной потенциальнои 
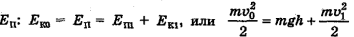, или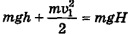 
.
На рис. 15-2, а) тело скатывается с наклонной плоскости длиной I с углом при основании а без трения и без начальной скорости, т. е.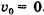 
. Закон сохранения механической энергии применительно к этому случаю запишется так же, как и в случае, изображенном на рис. 15-1, а):
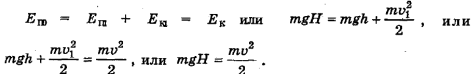
Здесь высота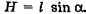 
.
На рис. 15-2, б) тело скатывается с наклонной плоскости, имея начальную скорость 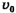. Этот случай соответствует случаю, изображенному на рис. 15-1, б):
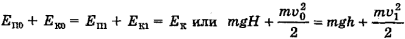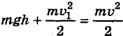, или 
, или 
, где v — скорость у основания наклонной плоскости.
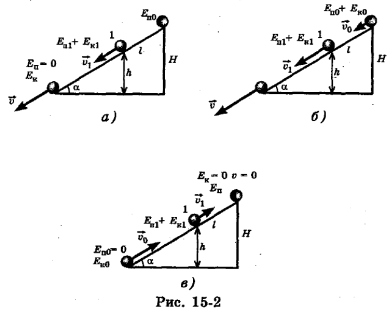
На рис. 15-2, в) тело вкатывается на наклонную плоскость с начальной скоростью 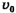и останавливается на высоте Н. Этот случай соответствует случаю, изображенному на рис. 15-1, в: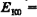 
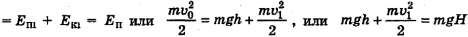или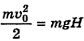 
.
Дополнительный пример:
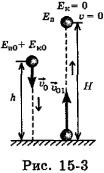
Тело брошено вниз с высоты h с начальной скоростью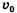 
и после абсолютно упругого удара подпрыгнуло на высоту Н (рис. 15-3).
Поскольку па высоте Н оно остановилось, там его конечная скорость стала равна нулю, то по закону сохранения механической энергии сумма его потенциальной 
и кинетической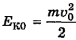 
энергий в начальном положении на высоте h равна его потенциальной энергии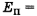 
в высшей точке подъема после удара, т. е. на высоте 
.
Если тело уронить свободно без начальной скорости с высоты Н, то после абсолютно упругого удара оно подпрыгнет на прежнюю высоту.
В примере 4 сумма потенциальной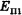 
и кинетической 
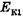энергий тела на любой промежуточной высоте равна сумме начальных потенциальной 
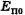и кинетической 
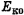энергий или равна конечной потенциальной энергии 
.
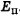Дополнительный пример:
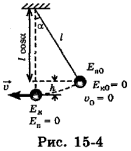
На рис. 15-4 шарик массой m, подвешенный на нити длиной l, отклонили от положения равновесия на угол а и отпустили.
В начальный момент шарик приобрел потенциальную энергию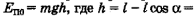 
— высота, на которую подняли шарик при отклонении. При движении шарика к бывшему положению равновесия его потенциальная энергия станет превращаться в кинетическую, которая в низшей точке будет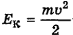 
. Если нет трения в точке подвеса и сопротивления среды, то по закону сохранения механической энергии 
.
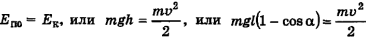Дополнительный пример:
Пружина жесткостью k растянута так, что ее деформация равна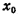 
(рис. 15-5). При этом шарику массой m, прикрепленному к свободному концу пружины, сообщена потенциальная энергия 
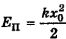. При возвращении шарика под действием силы упругости к прежнему положению равновесия с нулевой деформацией пружины его потенциальная энергия уменьшается,
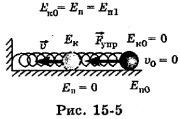
а кинетическая увеличивается, и при нулевой деформации потенциальная энергия полностью превращается в кинетическую: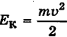 
. По закону сохранения механической энергии
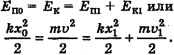
Здесь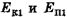 
— кинетическая и потенциальная энергии шарика в любом промежуточном положении.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
