Пример решения задачи №1.
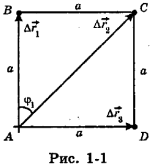
Часовой охраняет объект, огороженный квадратным забором ABCD (рис. 1-1), обходя его по периметру. Чему будут равны его путь и перемещение, если он из точки А перейдет в точку В, затем в точку С, затем в точку D, после чего вернется в точку А? Длина стороны квадрата а.
Решение:
1) Часовой перешел из точки А в точку В. Вектор его перемещения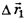 
направлен из точки А в точку В, а модуль перемещения 
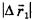равен пути S: и равен длине стороны квадрата АВ:
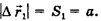
2) Часовой перешел из точки А в точку С. Вектор его перемещения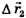 
направлен из точки А в точку С.
В этом случае путь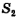 
равен сумме длин сторон АВ и ВС:
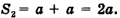
Модуль вектора перемещения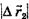 
равен длине диагонали АС. Из прямоугольного треугольника ACD согласно теореме Пифагора следует:
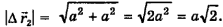
Поскольку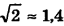 
(полезно запомнить), то
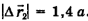
3) Часовой перешел из точки А в точку D. Пройденный им путь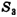 
в этом случае равен сумме длин трех сторон АВ, ВС и CD,
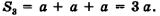
Модуль вектора перемещения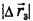 
равен длине стороны AD и направлен из точки А в точку D,
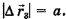
4) Часовой вернулся в точку А, полностью обойдя забор по периметру. Пройденный им путь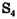 
равен длине периметра ABCDX
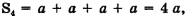
а перемещение равно нулю.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
