Движение с переменным ускорением

Движение с переменным ускорением

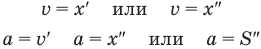
Здесь 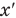— первая производная координаты по времени (м/с), 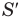— первая производная пути по времени (м/с), 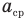— среднее ускорение 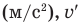— первая производная скорости по времени 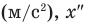— вторая производная координаты по времени 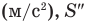— вторая производная пути по времени 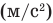. Остальные величины названы в пункте Равноускоренное движение.

Правило сложения классических скоростей:

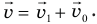
Здесь 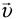— скорость тела относительно неподвижной системы отсчета (абсолютная скорость), 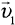— скорость тела относительно подвижной системы отсчета (относительная скорость), 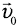— скорость подвижной системы отсчета относительно неподвижной (переносная скорость).

Если из условия задачи следует, что тело начало движение из состояния покоя, например, поезд отошел от станции или автомобиль выехал из пункта А и т. п., то в «Дано:» следует записать, что его начальная скорость 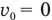. Если же из условия задачи следует, что тело в конце торможения остановилось, то следует записать, что его конечная скорость v = 0.

Из сравнения уравнений

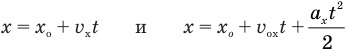
следует, что если координата тела х зависит от времени движения t в первой степени, то это равномерное движение, а если координата х зависит от времени 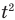, то это движение равноускоренное. Если же координата тела зависит от времени с иным показателем степени, то такое движение происходит с переменным ускорением и к нему формулы равноускоренного движения неприменимы (кроме формулы 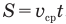, которую можно использовать при любом движении). Аналогично, если скорость тела зависит от времени движения в первой степени, как в формуле 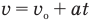, то движение равноускоренное, а если показатель степени у времени t нулевой, то 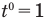, и это значит, что скорость не зависит от времени, т.е. постоянна, поэтому движение является равномерным. Если же показатель степени у скорости иной, то движение происходит с переменным ускорением.

Если вам дано уравнение типа 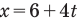(см), то из сравнения его с уравнением 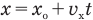следует, что начальная координата 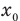= 6 см, а скорость тела v = 4 см/с.

Если вам дано уравнение типа 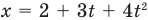(м), то из сравнения его с уравнением 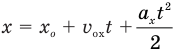следует, что начальная координата 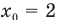м, проекция начальной скорости 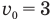м/с и, так как 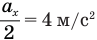, проекция ускорения тела .

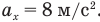Формулу средней скорости 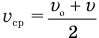можно применять только при равноускоренном движении, т.е. когда ускорение тела не меняется в течение всего времени движения. Если же на некотором пути тело двигалось сначала с одним ускорением, потом с другим или вообще равномерно, то определять среднюю скорость на всем пути или за все время движения можно только из формулы

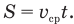
Пути, проходимые телом при равноускоренном движении без начальной скорости, относятся как ряд последовательных нечетных чисел:

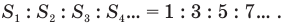
Если в условии задачи идет речь о скорости в средней точке пути, то учтите, что это не средняя скорость на всем пути, а мгновенная скорость на середине пути, — она является конечной скоростью для первой половины пути и начальной скоростью для второй половины.

Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

Теория относительности в физике: основные формулы

Виды прямолинейного движения в физике

Свободное падение в физике

Относительность движения в физике