Задача С14. Два теплоизолированных сосуда соединены узкой трубкой с закрытым краном, объемом которой можно пренебречь. В первом сосуде содержится 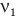 молей идеального газа со средней квадратичной скоростью молекул
молей идеального газа со средней квадратичной скоростью молекул 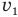 , а во втором содержится
, а во втором содержится 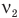 молекул этого газа со средней квадратичной скоростью молекул
молекул этого газа со средней квадратичной скоростью молекул 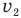 . Все молекулы одинаковы. Какова будет их средняя квадратичная скорость молекул и, если кран открыть?
. Все молекулы одинаковы. Какова будет их средняя квадратичная скорость молекул и, если кран открыть?
Обозначим 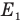 общую кинетическую энергию всех молекул в первом сосуде, когда кран был закрыт,
общую кинетическую энергию всех молекул в первом сосуде, когда кран был закрыт, 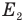 — общую кинетическую энергию всех молекул во втором сосуде, Е — общую кинетическую энергию всех молекул после того, как открыли кран,
— общую кинетическую энергию всех молекул во втором сосуде, Е — общую кинетическую энергию всех молекул после того, как открыли кран, 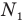 — число молекул в первом сосуде,
— число молекул в первом сосуде, 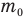 — массу каждой молекулы,
— массу каждой молекулы, 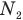 — число молекул во втором сосуде.
— число молекул во втором сосуде.

Решение:
Нам сказано, что сосуды теплоизолированы. Для чего это сказано? Наверно, чтобы дать понять, что суммарная энергия всех молекул в них после того, как открыли кран, никуда не денется, т.е. останется равной сумме энергий молекул в каждом сосуде, хотя энергия отдельных молекул станет иной. Речь идет, конечно, об их кинетических энергиях, ведь потенциальной энергии у молекул идеального газа нет, они не взаимодействуют на расстоянии. Тогда по закону сохранения энергии
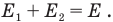
Энергию всех молекул в первом сосуде можно представить как произведение числа молекул N, в этом сосуде и кинетической энергии каждой молекулы, движущейся со скоростью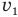 , которая равна
, которая равна  , а энергия всех молекул в этом сосуде
, а энергия всех молекул в этом сосуде
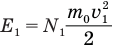
Аналогично кинетическая энергия всех 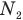 молекул в другом сосуде (когда он еще был закрыт) равна
молекул в другом сосуде (когда он еще был закрыт) равна
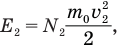
а кинетическая энергия всех молекул в обоих сосудах, которая останется неизменной, когда кран откроют, равна
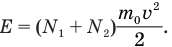
Подставим правые части этих равенств в первое уравнение. Так мы соединим искомую скорость v с известными скоростями 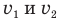 :
:
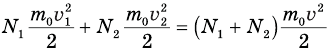
или после сокращений
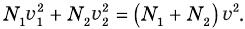
Отсюда 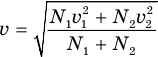 .
.
Но мы не знаем числа молекул 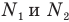 в обоих сосудах. Зато знаем число молей в каждом из них. А поскольку мы все формулы выучили назубок (а как иначе? — иначе о высоком балле на ЕГЭ можно и не мечтать), то сразу сообразим применить здесь формулу, которая позволит связать неизвестное число молекул с известным нам числом молей:
в обоих сосудах. Зато знаем число молей в каждом из них. А поскольку мы все формулы выучили назубок (а как иначе? — иначе о высоком балле на ЕГЭ можно и не мечтать), то сразу сообразим применить здесь формулу, которая позволит связать неизвестное число молекул с известным нам числом молей:
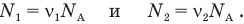
Подставим правые части этих формул в предыдущее равенство:
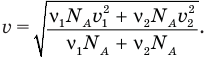
Нам осталось сократить число Авогадро, и задача будет решена:
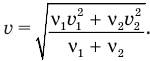
Ответ: 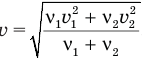 .
.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
