Задача В2. Вычислить среднюю квадратичную скорость молекул газа, если его масса m = 6 кг, объем 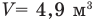 и давление р = 200 кПа.
и давление р = 200 кПа.
Обозначим  среднюю квадратичную скорость молекул,
среднюю квадратичную скорость молекул, 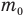 — массу каждой молекулы газа, n — концентрацию молекул, N —все число молекул в этом объеме. Остальные величины обозначены в условии задачи.
— массу каждой молекулы газа, n — концентрацию молекул, N —все число молекул в этом объеме. Остальные величины обозначены в условии задачи.
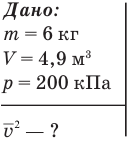
Решение:
Среднюю квадратичную скорость молекул газа найдем из основного уравнения кинетической теории, в которое входит и эта величина:
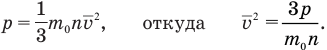
Концентрация молекул газа п равна отношению их числа N в объеме V к этому объему:
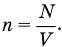
Подставим последнее выражение в предыдущую формулу и посмотрим, что получится:
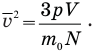
Произведение массы каждой молекулы 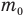 на их число N в объеме V равно массе m всех молекул в этом объеме, которая нам известна. Значит, заменив произведение
на их число N в объеме V равно массе m всех молекул в этом объеме, которая нам известна. Значит, заменив произведение 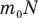 в знаменателе последней формулы на массу всего газа т, мы решим задачу в общем виде:
в знаменателе последней формулы на массу всего газа т, мы решим задачу в общем виде:
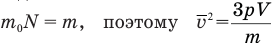
Выразим единицу давления в СИ:

Произведем вычисления:
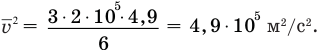
Ответ: 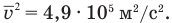 .
.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
