Задача С19. С края полусферы радиусом R, вершина которой лежит на горизонтальной плоскости, по внутренней поверхности полусферы скатывается без трения маленький кубик массой т и ударяется о другой маленький кубик вдвое большей массы, лежащий в самом низу полусферы. Какое количество теплоты выделится в результате неупругого удара?
Обозначим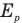 
— потенциальную энергию кубика массой m на краю полусферы, 
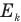— кинетическую энергию этого кубика в нижней точке полусферы перед ударом, 
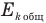— общую кинетическую энергию кубиков сразу после удара, Q — количество теплоты, выделившееся в результате удара, g — ускорение свободного падения, v — скорость скатившегося кубика непосредственно перед ударом, 
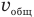— общую скорость кубиков сразу после удара.
Решение:
По закону сохранения энергии количество теплоты, выделившейся в результате неупругого соударения кубиков, равно разности их общей кинетической энергии сразу после удара и потенциальной энергии кубика на краю полусферы:
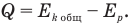
Общую кинетическую энергию и потенциальную энергию определим по формулам
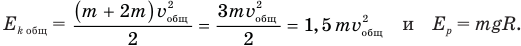
С учетом этих равенств
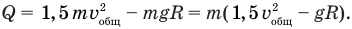
Общую скорость кубиков сразу после удара найдем по закону сохранения импульса. Согласно этому закону импульс скатившегося кубика непосредственно перед ударом равен суммарному импульсу обоих кубиков сразу после удара:
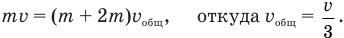
Скорость скатившегося кубика перед ударом найдем по закону сохранения механической энергии, согласно которому потенциальная энергия кубика на краю полусферы равна его кинетической энергии перед ударом:
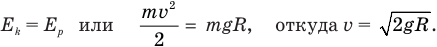
Подставим правую часть этого равенства в выражение (2):
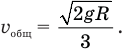
Нам осталось подставить правую часть равенства (3) в формулу (1).
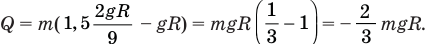
Знак «минус» свидетельствует о том, что механическая энергия кубиков уменьшилась.
Ответ: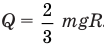 
.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
