Задача C17. Небольшое тело соскальзывает с вершины полусферы радиусом R (рис. 136). На какой высоте h тело сорвется с поверхности полусферы и полетит вниз? Трение не учитывать.
Обозначим g ускорение свободного падения, 
— начальную скорость тела на вершине полусферы, 
— потенциальную энергию тела на вершине полусферы, 
— потенциальную энергию тела на высоте 
— кинетическую энергию тела на высоте 
— линейную скорость тела в момент отрыва от поверхности, m — массу тела, 
— угол между радиусом, соединяющим тело с центром полусферы, и вертикалью, 
— центростремительное ускорение тела.
Решение:
По закону сохранения механической энергии потенциальная энергия тела 
на вершине полусферы, т.е. на высоте, равной радиусу полусферы R, равна сумме его потенциальной 
и кинетической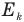 
энергий в любой другой точке, и значит, и в момент отрыва тела на высоте h:
Здесь 
.
Тогда
Для нахождения высоты h нам требуется определить линейную скорость тела V. Для этого воспользуемся вторым законом Ньютона. В момент отрыва тела от поверхности полусферы на него действует только сила тяжести 
, а сила реакции опоры становится равной нулю. Тело еще движется по окружности, поэтому центростремительное ускорение в каждой точке направлено по радиусу к центру полусферы. Спроецируем силу тяжести на радиус, соединяющий тело с центром полусферы в момент отрыва. Проекция 
по второму закону Ньютона равна:
Поскольку
Но угол о. нам тоже не известен. Однако, если внимательно посмотреть на чертеж, то можно заметить такой же угол между вектором силы тяжести и радиусом, проведенным к телу в момент отрыва. Эти углы равны как накрест лежащие при параллельных и секущей. Из линейного прямоугольного треугольника с гипотенузой R и прилежащим к углу а катетом h следует, что
Тогда
Подставив (2) в (1), получим:
откуда
Ответ: 
.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
