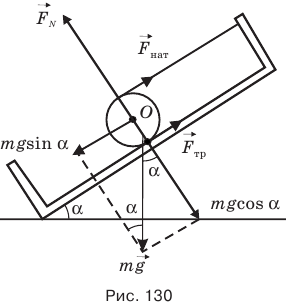
Задача С6. На дне ящика находится шар, удерживаемый нитью в равновесии (рис. 130). На какой максимальный угол можно отклонить ящик от горизонтальной поверхности, чтобы шар остался в равновесии, если коэффициент трения шара о дно ящика равен 0,5? Весом нити пренебречь.

Задача С6. На дне ящика находится шар, удерживаемый нитью в равновесии (рис. 130). На какой максимальный угол можно отклонить ящик от горизонтальной поверхности, чтобы шар остался в равновесии, если коэффициент трения шара о дно ящика равен 0,5? Весом нити пренебречь.

Обозначим 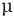коэффициент трения, 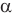— максимальный угол, на который можно отклонить ящик, m — массу шара, g — ускорение свободного падения, 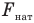— силу натяжения нити, 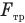— силу трения, 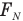— силу реакции опоры, R — радиус шара, g — ускорение свободного падения.

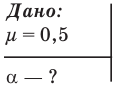
Решение:

Выполним чертеж, на котором покажем все силы, приложенные к шару. На него действуют: сила тяжести 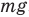, сила трения 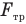, сила реакции опоры 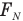и сила натяжения нити 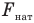. Разложим силу тяжести на скатывающую и прижимающую к дну ящика 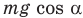. При равновесии шара 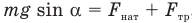, а также согласно равенству моментов сил трения и натяжения относительно оси вращения, проходящей через точку О,

откуда .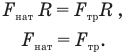

Здесь R — радиус шара, который является плечом сил трения и натяжения.

С учетом этого, ,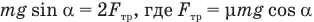

поэтому ,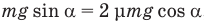

откуда .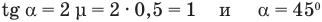

Ответ: .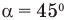

Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти задачи:

Задача C4. Гиря, положенная сверху на вертикальную пружину, сжимает ее на 1 мм. Если эту гирю бросить на пружину со скоростью 0,2 м/с с высоты 10 см, то какова теперь будет деформация пружины?

Задача С5. Через невесомый блок перекинута нить, к концам которой прикреплены грузы кг. К грузу массой подвесили на нити груз массой кг (рис. 129). Найти силу натяжения нити между грузами.

Задача C7. Шарик из материала, плотность которого в n раз меньше плотности воды, падает в воду с высоты Н. На какую максимальную глубину h погрузится шарик?

Задача С8. Два одинаковых бруска массами по 20 г каждый соединены упругой вертикальной пружиной с жесткостью 300 Н/м (рис. 131, а). Нажатием на верхний брусок пружину сжали так, что ее деформация стала 5 см (рис. 140, б). Какова будет скорость центра масс этой системы тел в момент отрыва нижнего бруска от стола? Сопротивление не учитывать.