Задача С10. Сбегая по эскалатору с одной скоростью, мальчик насчитал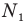 
ступенек, а когда он увеличил скорость в полтора раза, он насчитал на SN ступенек больше. Сколько ступенек N насчитает мальчик, спускаясь с первой скоростью по неподвижному эскалатору?
Обозначим 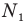число ступенек, которое насчитал мальчик, сбегая по эскалатору со скоростью 
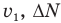— разница между числом ступенек, которое насчитает мальчик, сбегая со скоростью 
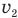, и числом ступенек, которое он насчитает, сбегая со скоростью 
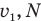— число ступенек, которое насчитает мальчик, спускаясь по неподвижному эскалатору, h — ширину ступеньки эскалатора.
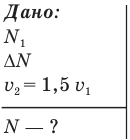
Решение:
Пусть и ширина, и высота ступеньки эскалатора h. Тогда путь, пройденный мальчиком за некоторое время t со скоростью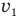 
в системе отсчета, связанной с неподвижными объектами, например, с поручнями эскалатора, равен hN. Ведь N это число ступенек, которое содержит вся лента эскалатора, и именно столько ступенек насчитает мальчик, спускаясь по неподвижному эскалатору.
Время спуска, при условии, что мальчик движется равномерно, равно:
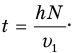
В системе отсчета, связанной с движущейся лентой эскалатора, мальчик за это же время t пробежит путь, равный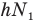 
спускаясь с собственной скоростью 
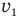, плюс скорость эскалатора 
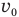(заметим, что чем быстрее он бежит в ту же сторону, что и эскалатор, тем больше ступенек успеет насчитать за время спуска. А если бы он не бежал, то насчитал бы всего одну ступеньку, ту, на которой стоял). С учетом этого
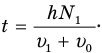
Приравняв правые части равенств (1) и (2), мы «уйдем» от неизвестного времени t:
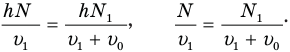
Когда мальчик увеличил свою скорость в полтора раза, т.е. стал бежать со скоростью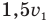 
, то успел насчитать на 
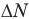ступенек больше, т.е. теперь он насчитал 
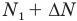ступенек. Рассуждая аналогично, мы можем сразу записать уравнение (4), подобное уравнению (3), заменив в нем 
:
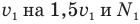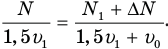
Нам осталось исключить неизвестные скорости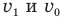 
из уравнений (3) и (4). И хоть мы имеем всего два уравнения с тремя неизвестными величинами, мы попытаемся определить А. Для начала найдем из уравнения (3) 
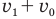а из уравнения (4) 
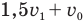воспользовавшись правилом пропорции:
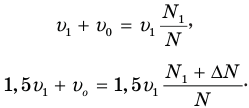
Если теперь из уравнения (6) вычесть уравнение (5), то «уйдет» скорость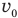 
, а скорость 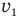в правой части будущего уравнения можно будет вынести за скобки и сократить с той 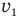, что останется в левой части этого уравнения. Проделаем эти действия:
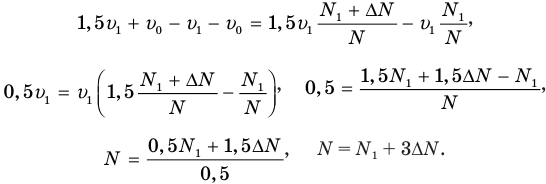
Ответ: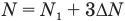 
.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
