Пусть в некоторой замкнутой области  плоскости
плоскости 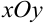 определена ограниченная функция
определена ограниченная функция 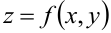 , причём
, причём 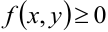 . К определению двойного интеграла приходим, вычисляя объём фигуры, основание которой — область
. К определению двойного интеграла приходим, вычисляя объём фигуры, основание которой — область  ; сверху фигура ограничена поверхностью, уравнение которой
; сверху фигура ограничена поверхностью, уравнение которой 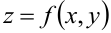 ; боковая поверхность — цилиндрическая, образованная прохождением прямой, параллельной оси
; боковая поверхность — цилиндрическая, образованная прохождением прямой, параллельной оси 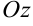 вдоль границы
вдоль границы 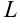 области
области  . Такая фигура называется цилиндрическим телом (рисунок 10.1).
. Такая фигура называется цилиндрическим телом (рисунок 10.1).
Объём цилиндрического тела можно вычислить приближённо, заменив его ступенчатой фигурой следующим образом.
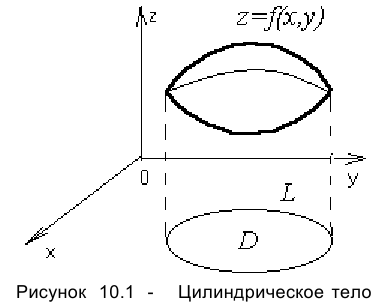
1. Область  произвольным образом разбивается на конечное число
произвольным образом разбивается на конечное число 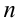 элементарных областей (ячеек)
элементарных областей (ячеек) 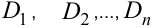 , площади которых обозначим соответственно
, площади которых обозначим соответственно 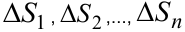 .
.
Диаметром ячейки называют наибольшее расстояние между двумя точками на её границе и обозначают 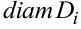 .
.
2. Выберем в каждой ячейке 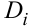 произвольную точку
произвольную точку 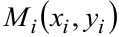 и вычислим в ней значение
и вычислим в ней значение 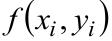 . Составим сумму вида:
. Составим сумму вида:

Каждое слагаемое в сумме (10.1) вычисляет объём прямого цилиндра с основанием 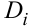 и высотой
и высотой 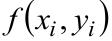 . Сумма (10.1) называется интегральной суммой для функции
. Сумма (10.1) называется интегральной суммой для функции  по области
по области  . Предел интегральной суммы (10.1) при
. Предел интегральной суммы (10.1) при 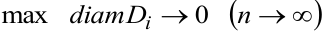 называется двойным интегралом от функции
называется двойным интегралом от функции  по области
по области  :
:
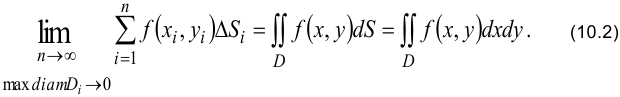
В обозначении двойного интеграла  — область интегрирования,
— область интегрирования,  — подынтегральная функция,
— подынтегральная функция, 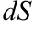 — дифференциал площади, который можно заменить произведением дифференциалов независимых переменных
— дифференциал площади, который можно заменить произведением дифференциалов независимых переменных 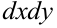 .
.
Формула (10.2) позволяет вычислить объём цилиндрического тела при 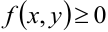 , в чём и заключается геометрический смысл двойного интеграла.
, в чём и заключается геометрический смысл двойного интеграла.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
