Если каждой паре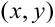 
значений двух, независимых друг от друга, переменных величин 
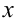и 
, и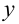з некоторой области их изменения 
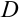, по закону 
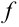ставится в соответствие определённое значение величины 
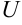, то говорят, что 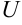есть функция двух переменных 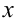и 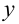, определённая в области 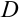. Функция двух переменных обозначается так: 
.
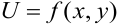Функция может иметь не только две, но и три и более независимых переменных, например,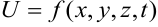 
.
Всё новое, что возникает в дифференциальном исчислении при переходе от функции одной переменной к функции нескольких переменных, свойственно уже функции двух переменных. Поэтому рассматриваем функцию двух переменных с кратким обобщением на функции нескольких переменных.
Совокупность пар 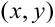значени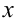й и 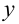, при которых определяется функция 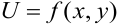, называется областью существования или областью определения этой функции. При этом пара 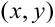определяет точку 
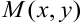в области существования. Следовательно, область определения — часть плоскости 
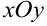. Окрестностью точки 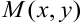является открытый круг малого радиуса с центром в этой точке.
Функцию двух переменных можно рассматривать, как функцию точки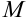 
: 
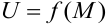. Если задана функция 3-х переменных, 
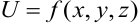, то одно значение трех переменных 
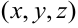определяет точку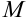 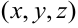в пространстве. Функцию 3-х переменных, 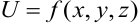, можно снова рассматривать как функцию точки, но уже в трехмерном пространстве .
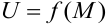Область определения обладает свойствами связности и открытости.
Свойство связности заключается в том, что две точки, принадлежащие области можно соединить непрерывной линией, полностью лежащей в области.
Свойство открытости заключается в том, что любая точка области входит в неё вместе со своей окрестностью.
Границей области называется точка или множество точек, не принадлежащих области, но в окрестности которых имеются точки, принадлежащие области. Например, если область 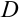задана неравенством 
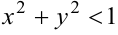(открытый круг радиусом 1), то граница области — окружность 
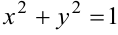. Если граница присоединена к области, то область называется замкнутой.
В области 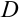существует множество точек, в которых функция 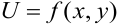, принимает одинаковые значения. Пусть 
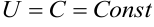. Тогда уравнение 
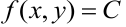определяет линию в плоскости 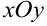, во всех точках которой 
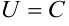. Такая линия называется линией уровня. Если задана функция трёх переменных 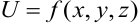, то уравнение 
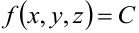определяет поверхность в пространстве, во всех точках которой 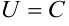. Такая поверхность называется поверхностью уровня.
Пример:
Пусть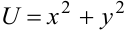 
. Значениям функции 
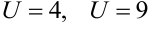соответствуют линии уровня 
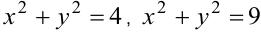. Запишем уравнения в виде 
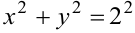и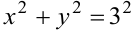 
. Это уравнения окружностей с центром в начале координат и радиусом 2 и 3 соответственно.
Понятие предела и непрерывности функции нескольких переменных логически связано с такими же понятиями для функции одной переменной (см. материал 1-го семестра).
Функцию нескольких переменных будем рассматривать, как функцию точки 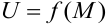, что позволит сформулировать определение, пригодное для функций с различным числом независимых переменных.
Определение 1. Число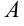 
называется пределом функци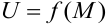и при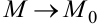 
, если для каждого числа 
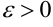найдется такое число 
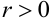, что для всех точек 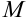, для которых выполняется неравенство 
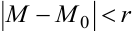, имеет место неравенство 
.
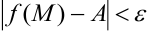При этом пишут: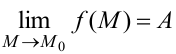 
.
Определение 2. Функция 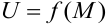называется непрерывной в точке 
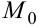, если она определена в этой точке и в её окрестности, и если существует предел 
, равный значению функции в этой точке,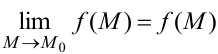 
.
Особенностью определений 1 и 2 заключается в том, что при 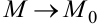движение точки 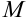может происходить по любой траектории в окрестности точки 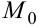, т.е. на плоскости в случае двух независимых переменных, в пространстве в случае трёх независимых переменных.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
