Пусть требуется вычислить интеграл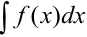 
, причем первообразную нельзя подобрать непосредственно по таблице. Сделаем замену переменной по формуле 
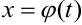, где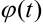 
— непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда справедливо равенство
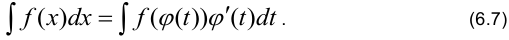
Равенство (6.7) подразумевает, что после интегрирования в правой части равенства вместо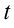 
будет подставлено выражение через 
.
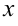Пример №1
Найти интеграл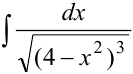 
.
Решение:
В последующем изложении показано, что для такого интеграла нужно применить подстановку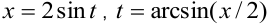 
. Тогда 
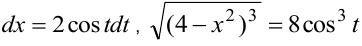. Интеграл с новой переменной — табличный: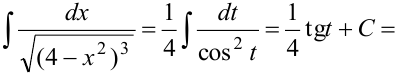 
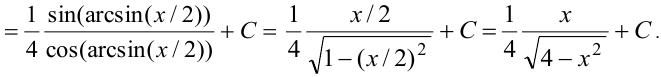
Иногда замену переменной целесообразнее подбирать не по формуле 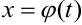, а по формуле 
.
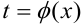Пример №2
Найти интеграл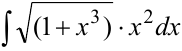 
.
Решение:
Обозначим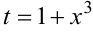 
. Тогда 
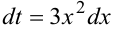. Умножим и разделим интеграл на 3, получим
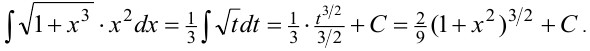
При подстановке 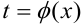применяется приём подведения функции под знак дифференциала, основанный на свойстве №6. С учётом того, что дифференциал функции определяется по формуле
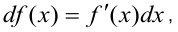
в подынтегральном выражении нужно отыскать функцию, которую принимаем за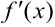 
и подводим под знак дифференциала.
Пример №3
Найти интеграл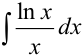 
.
Решение:
В подынтегральном выражении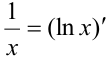 
, поэтому 
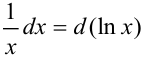, выражение подводится под знак дифференциала. Затем выбираем подстановку 
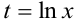, которая делает интеграл табличным.
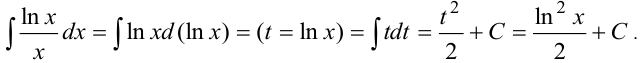
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Таблица интегралов и табличное интегрирование |
| Интегрирование по частям |
| Интегрирование простейших рациональных дробей |
| Разложение многочлена на множители |
