Определение 1. Функция 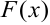 называется первообразной от функции
называется первообразной от функции 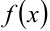 на отрезке
на отрезке 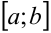 , если для всех
, если для всех 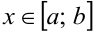 выполняется равенство
выполняется равенство

Определение первообразной от заданной функции называется интегрированием этой функции. Интегрирование — действие обратное дифференцированию и практически более сложное.
Первообразная для заданной функции не является единственной. Так, 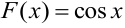 — первообразная для функции
— первообразная для функции 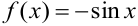 , так как
, так как 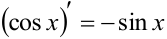 . Но и
. Но и 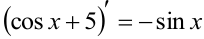 . Пример показывает, что если известна одна первообразная
. Пример показывает, что если известна одна первообразная 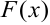 , то любая другая имеет вид
, то любая другая имеет вид 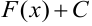 , где
, где 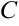 — произвольная постоянная.
— произвольная постоянная.
Теорема. Если 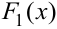 и
и 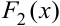 — две первообразные от функции
— две первообразные от функции 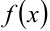 на отрезке
на отрезке 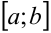 , то разность между ними равна постоянному числу.
, то разность между ними равна постоянному числу.
Определение 2. Если функция 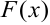 является первообразной для
является первообразной для 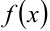 , то выражение
, то выражение 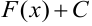 называется неопределённым интегралом и обозначается
называется неопределённым интегралом и обозначается

Здесь 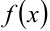 — подынтегральная функция,
— подынтегральная функция, 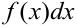 — подынтегральное выражение,
— подынтегральное выражение, 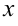 — переменная интегрирования,
— переменная интегрирования, 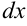 — дифференциал переменной интегрирования.
— дифференциал переменной интегрирования.
Из определений (6.1), (6.2) и правил дифференцирования вытекают свойства неопределённого интеграла:
1. Производная от неопределённого интеграла равна подынтегральной функции:
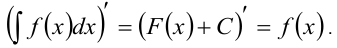
2. Дифференциал от неопределённого интеграла равен подынтегральному выражению:
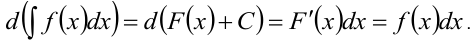
3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:
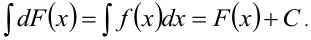
4. Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов этих функций: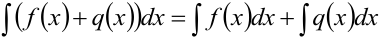 . Последнее равенство справедливо с точностью до произвольной постоянной. Если найти производные от левой и правой частей равенства
. Последнее равенство справедливо с точностью до произвольной постоянной. Если найти производные от левой и правой частей равенства 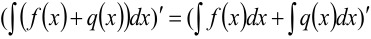 , то
, то 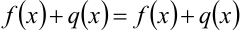 .
.
5. Постоянный множитель можно вынести за знак интеграла: 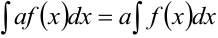 , где
, где 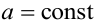 .
.
Следствие свойств 4 и 5 — неопределенный интеграл линейной комбинации конечного числа функций равен линейной комбинации интегралов этих функций (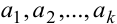 — постоянные числа):
— постоянные числа):
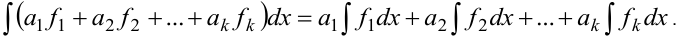
6. Если 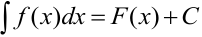 , то
, то 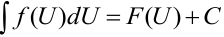 , где
, где 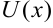 — произвольная дифференцируемая функция. Это свойство есть следствие свойства инвариантности формы дифференциала функции, согласно которому
— произвольная дифференцируемая функция. Это свойство есть следствие свойства инвариантности формы дифференциала функции, согласно которому 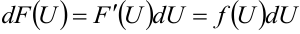 , если
, если 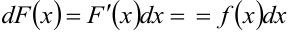 .
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Дифференциал функции, его свойства и применение |
| Применение 1-й и 2-й производной для исследования функций |
| Таблица интегралов и табличное интегрирование |
| Интегрирование по частям |
